Building a Tango puzzle solver with Z3
Tango is an engaging logic game played on a square grid. In this post, we’ll explore the rules of the game and build a solver using Python’s Z3 theorem prover. We’ll also create a nice visualization of the solutions using matplotlib.
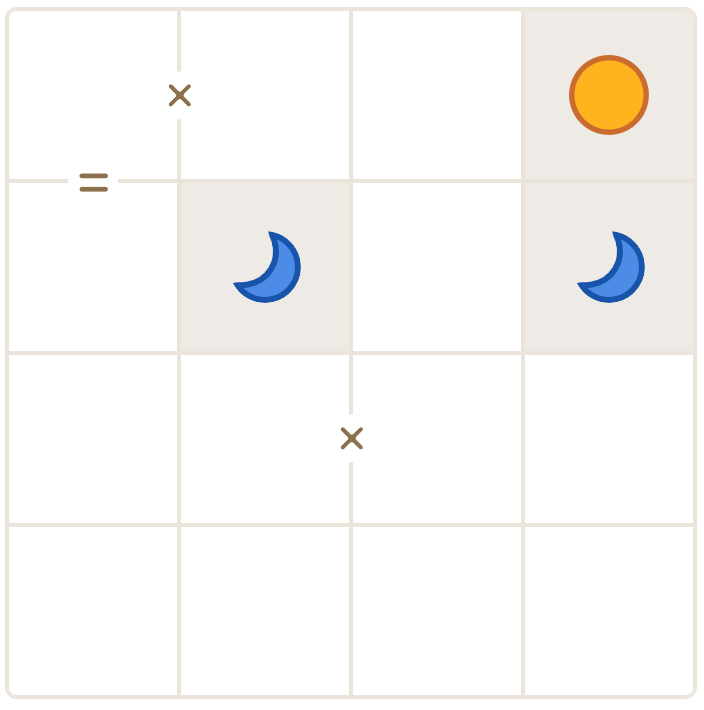
Game Rules
The puzzle is played on an n×n grid where each cell must contain either a sun (☀️) or a moon (🌙). The rules are:
-
Adjacent Symbols: No more than two suns or moons can be adjacent to each other, either horizontally or vertically. For example:
- ☀️☀️ is allowed
- ☀️☀️☀️ is not allowed
- The same applies to moons
-
Balance Rule: Each row and column must contain an equal number of suns and moons
-
Equal Signs: Cells connected by an = sign must contain the same symbol
-
Opposite Signs: Cells connected by an X sign must contain opposite symbols
-
Unique Solution: Each puzzle has exactly one solution that can be found through logical deduction
Implementation with Z3
Let’s break down how we implement each rule using Z3. We’ll start by creating boolean variables for each cell, where True represents a sun and False represents a moon.
Setting Up the Grid
def solve_tango(size, equals_constraints, opposite_constraints, initial_suns=None, initial_moons=None):
solver = Solver()
# Create boolean variables for each cell
cells = [[Bool(f"cell_{i}_{j}") for j in range(size)] for i in range(size)]
Rule 1: Adjacent Symbols
To implement the “no more than 2 adjacent symbols” rule, we need to check every sequence of three cells horizontally and vertically. We use Z3’s Sum and If functions to count the number of suns:
def count_suns(cell_list):
return Sum([If(cell, 1, 0) for cell in cell_list])
# Check horizontal sequences
for i in range(size):
for j in range(size-2):
# No more than 2 suns in any 3 consecutive cells
solver.add(count_suns([cells[i][j], cells[i][j+1], cells[i][j+2]]) <= 2)
# No more than 2 moons (equivalent to at least 1 sun)
solver.add(count_suns([cells[i][j], cells[i][j+1], cells[i][j+2]]) >= 1)
# Similar checks for vertical sequences
Rule 2: Balance Rule
To ensure equal numbers of suns and moons in each row and column, we count the suns and set them equal to half the grid size:
half_size = size // 2
for i in range(size):
# Each row must have exactly half suns
solver.add(count_suns(cells[i]) == half_size)
# Each column must have exactly half suns
solver.add(count_suns([cells[j][i] for j in range(size)]) == half_size)
Rules 3 & 4: Equal and Opposite Signs
These constraints are straightforward to implement using Z3’s boolean operations:
# Equal signs constraints
for (i1, j1), (i2, j2) in equals_constraints:
solver.add(cells[i1][j1] == cells[i2][j2])
# Opposite signs constraints
for (i1, j1), (i2, j2) in opposite_constraints:
solver.add(cells[i1][j1] != cells[i2][j2])
Initial Placements
To handle pre-placed suns and moons:
if initial_suns:
for i, j in initial_suns:
solver.add(cells[i][j] == True)
if initial_moons:
for i, j in initial_moons:
solver.add(cells[i][j] == False)
Visualization
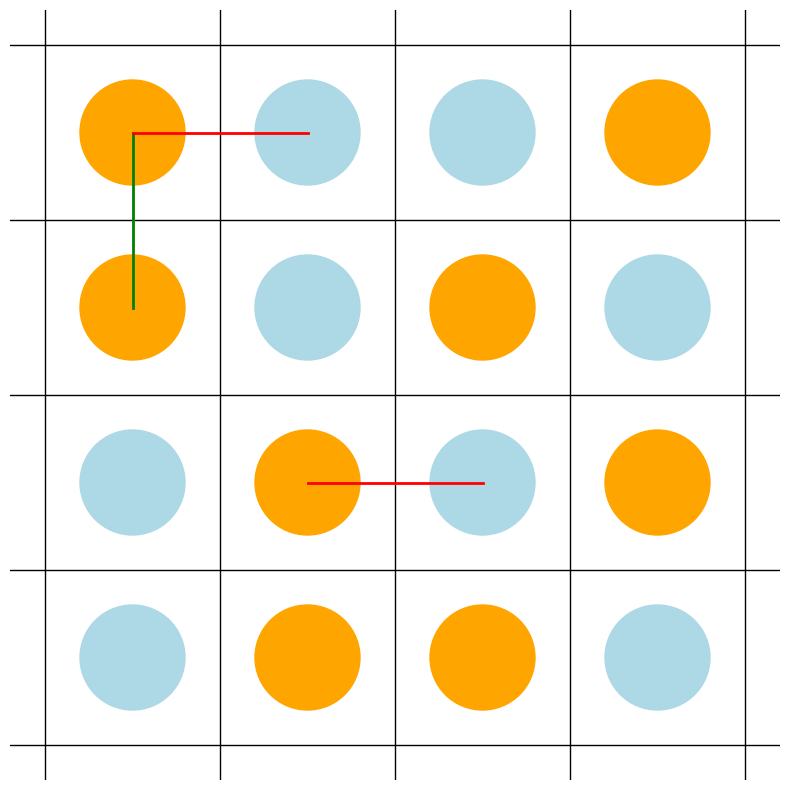
We use matplotlib to create a clear visualization of the puzzle and its solution. The visualization includes:
- Orange circles for suns
- Blue circles for moons
- Green lines for equal constraints
- Red lines for opposite constraints
- Different opacity levels for initial vs. solved cells
Here’s how we draw the symbols:
def visualize_solution(solution, equals_constraints, opposite_constraints, initial_suns=None, initial_moons=None):
size = len(solution)
fig, ax = plt.subplots(figsize=(8, 8))
# Draw grid lines
for i in range(size + 1):
ax.axhline(i, color='black', linewidth=1)
ax.axvline(i, color='black', linewidth=1)
# Draw symbols
for i in range(size):
for j in range(size):
is_initial = (initial_suns and (i, j) in initial_suns) or \
(initial_moons and (i, j) in initial_moons)
if solution[i][j]: # Sun
circle = plt.Circle((j + 0.5, size - i - 0.5), 0.3,
color='orange',
alpha=1 if is_initial else 0.7)
ax.add_artist(circle)
else: # Moon
circle = plt.Circle((j + 0.5, size - i - 0.5), 0.3,
color='lightblue',
alpha=1 if is_initial else 0.7)
ax.add_artist(circle)
Complete Implementation
Here is a puzzle and its solution using the code below:

from z3 import *
import matplotlib.pyplot as plt
import numpy as np
def solve_tango(size, equals_constraints, opposite_constraints):
# Create Z3 solver
solver = Solver()
# Create variables for each cell (True = Sun, False = Moon)
cells = [[Bool(f"cell_{i}_{j}") for j in range(size)] for i in range(size)]
# Helper to count suns in a list of cells
def count_suns(cell_list):
return Sum([If(cell, 1, 0) for cell in cell_list])
# Rule 1: No more than 2 suns/moons adjacent
for i in range(size):
for j in range(size-2):
# Horizontal check for suns
solver.add(count_suns([cells[i][j], cells[i][j+1], cells[i][j+2]]) <= 2)
solver.add(count_suns([cells[i][j], cells[i][j+1], cells[i][j+2]]) >= 1)
# Vertical check for suns
solver.add(count_suns([cells[j][i], cells[j+1][i], cells[j+2][i]]) <= 2)
solver.add(count_suns([cells[j][i], cells[j+1][i], cells[j+2][i]]) >= 1)
# Rule 2: Equal number of suns and moons in each row and column
half_size = size // 2
for i in range(size):
# Rows
solver.add(count_suns(cells[i]) == half_size)
# Columns
solver.add(count_suns([cells[j][i] for j in range(size)]) == half_size)
# Rule 3: Equal signs constraints
for (i1, j1), (i2, j2) in equals_constraints:
solver.add(cells[i1][j1] == cells[i2][j2])
# Rule 4: Opposite signs constraints
for (i1, j1), (i2, j2) in opposite_constraints:
solver.add(cells[i1][j1] != cells[i2][j2])
if initial_suns:
for i, j in initial_suns:
solver.add(cells[i][j] == True)
if initial_moons:
for i, j in initial_moons:
solver.add(cells[i][j] == False)
# Check if solution exists
if solver.check() == sat:
model = solver.model()
solution = [[model.evaluate(cells[i][j]) for j in range(size)]
for i in range(size)]
return solution
return None
def visualize_solution(solution, equals_constraints, opposite_constraints):
size = len(solution)
fig, ax = plt.subplots(figsize=(8, 8))
# Draw grid
for i in range(size + 1):
ax.axhline(i, color='black', linewidth=1)
ax.axvline(i, color='black', linewidth=1)
# Draw symbols
for i in range(size):
for j in range(size):
if solution[i][j]: # Sun
circle = plt.Circle((j + 0.5, size - i - 0.5), 0.3,
color='orange')
ax.add_artist(circle)
else: # Moon
circle = plt.Circle((j + 0.5, size - i - 0.5), 0.3,
color='lightblue')
ax.add_artist(circle)
# Draw constraints
for (i1, j1), (i2, j2) in equals_constraints:
y1, y2 = size - i1 - 0.5, size - i2 - 0.5
ax.plot([j1 + 0.5, j2 + 0.5], [y1, y2], 'g-', linewidth=2)
for (i1, j1), (i2, j2) in opposite_constraints:
y1, y2 = size - i1 - 0.5, size - i2 - 0.5
ax.plot([j1 + 0.5, j2 + 0.5], [y1, y2], 'r-', linewidth=2)
ax.set_aspect('equal')
ax.axis('off')
plt.tight_layout()
plt.show()
# Example usage for a 4x4 puzzle:
size = 4
equals_constraints = [((0, 0), (1, 0))]
opposite_constraints = [((0, 0), (1, 0)),((2,1), (2, 2))]
initial_suns = [(3, 0)]
initial_moons = [(1, 1), (3, 3)]
solution = solve_tango(size, equals_constraints, opposite_constraints)
if solution:
visualize_solution(solution, equals_constraints, opposite_constraints)
else:
print("No solution exists")
Future Improvements
Some possible enhancements to consider:
- Adding an interactive GUI for puzzle input.
- Implementing a puzzle generator.
- Adding difficulty ratings.
Conclusion
The tango puzzle provides an excellent example of how constraint satisfaction problems can be solved using Z3. The combination of logical constraints and visual representation makes it both an interesting programming challenge and an engaging puzzle to solve.
The solver we’ve built can handle puzzles of any size and includes support for initial placements, making it a versatile tool for both solving and creating new puzzles. The visualization helps users understand the solution and verify that all constraints are satisfied.