Number Hooks

Number hooks

In the grid below, enter nine 9’s in the outermost hook, eight 8’s in the next hook, then seven 7’s, six 6’s, and so on, down to the one 1 (already entered), so that the row and column sums match the values given along the border.

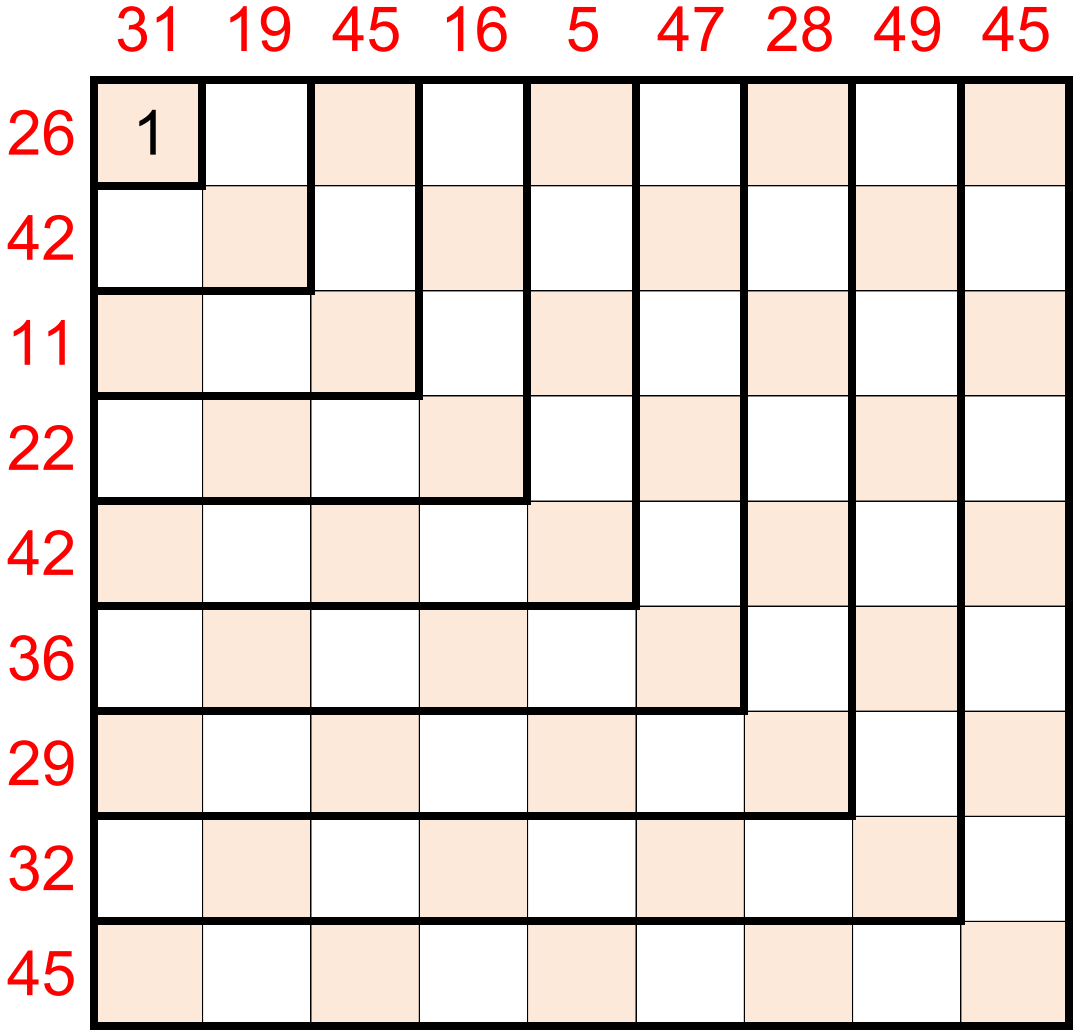
Solution

The code below provides the following solution to the above puzzle:

1 . 3 . . 6 7 . 9
2 2 3 . 5 6 7 8 9
3 . . . . . . 8 .
4 4 4 4 . 6 . . .
5 5 5 5 . 6 7 . 9
. . 6 . . 6 7 8 9
7 . 7 7 . . . 8 .
. 8 8 . . 8 . 8 .
9 . 9 . . 9 . 9 9

Python code

from z3 import *

def generate_hooks(size):
    hooks = []
    for n in range(1, size + 1):
        hook = []
        for i in range(n):
            for j in range(n):
                if i == n - 1 or j == n - 1:
                    hook.append((i, j))
        hooks.append(hook)
    return hooks


row_sums = [26, 42, 11, 22, 42, 36, 29, 32, 45]
col_sums = [31, 19, 45, 16, 5, 47, 28, 49, 45]


def solve_number_hook_puzzle():
    solver = Solver()

    # Create a 9x9 grid of integer variables
    grid = [[Int(f"cell_{i}_{j}") for j in range(9)] for i in range(9)]

    
    # Add constraints for row and column sums
    for i in range(9):
        solver.add(Sum(grid[i]) == row_sums[i])
        solver.add(Sum([grid[j][i] for j in range(9)]) == col_sums[i])

    # Generate hooks
    hooks = generate_hooks(9)

    # Add constraints for the hooks
    for i, hook in enumerate(hooks):
        value = i + 1  # Values from 1 to 9
        cells_in_hook = [grid[r][c] for r, c in hook]
        solver.add(Sum([If(cell == value, 1, 0) for cell in cells_in_hook]) == value)
        for r, c in hook:
            solver.add(Or(grid[r][c] == value, grid[r][c] == 0))

    # Ensure all numbers are between 0 and 9 (0 for empty cells)
    for row in grid:
        for cell in row:
            solver.add(And(cell >= 0, cell <= 9))

    # Check if the puzzle is solvable
    if solver.check() == sat:
        model = solver.model()
        return [[model.evaluate(grid[i][j]).as_long() for j in range(9)] for i in range(9)]
    else:
        return None

# Solve the puzzle
solution = solve_number_hook_puzzle()

# Print the solution
if solution:
    for row in solution:
        print(" ".join(map(lambda x: str(x) if x != 0 else '.', row)))
else:
    print("No solution found.")