Dancer pairs

Dancer Pairs

$15$ dancers are standing in an equilateral triangle formation, with every dancer standing $1$ unit apart from her nearest neighbors. Each dancer chooses another who is $1$ unit away to pair up with, and all but $1$ dancer ends up as a part of a pair. An example of one such arrangement is presented here.

How many different sets of $7$ pairs are possible?

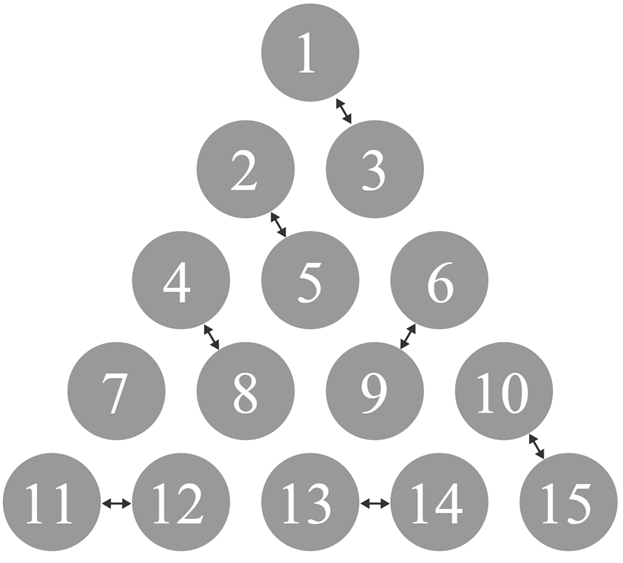
Solution

We use a backtracking algorithm in the generate_all_pairings function to generate all possible combinations. The backtrack function:

• Takes the current index, the current pairing, and the set of used nodes.

• If we have 7 pairs, we add the current pairing to our list of all pairings.

• For each node from the current index onwards:

  • If the node is already used, we skip it.

  • For each neighbor of the node:

    • If the neighbor is not used and has a higher index (to avoid duplicates), we create a new pairing with this pair.

    • We then recursively call backtrack with the updated pairing and used nodes.

• We use frozensets to represent pairs and combinations of pairs, allowing us to eliminate duplicates easily.

The code below shows us that there are $bold(240)$ ways of pairing the dancers. Here are a few sample pairings:

Python code

import networkx as nx
from itertools import combinations
import matplotlib.pyplot as plt
import math

def create_dancer_graph():
    G = nx.Graph()
    edges = [
        (1, 2), (1, 3),
        (2, 3), (2, 4), (2, 5),
        (3, 5), (3, 6),
        (4, 5), (4, 7), (4, 8),
        (5, 6), (5, 9), (5, 8),
        (6, 9), (6, 10),
        (7,8),(7, 11), (7, 12),
        (8, 9), (8, 13), (8,12),
        (9, 10), (9, 13), (9, 14),
        (10, 14), (10, 15),
        (11,12),(12,13),(13,14),(14,15)
    ]
    G.add_edges_from(edges)
    return G

def generate_all_pairings(G):
    all_pairings = []
    nodes = list(G.nodes())
    
    def backtrack(index, current_pairing, used_nodes):
        if len(current_pairing) == 7:
            all_pairings.append(frozenset(map(frozenset, current_pairing)))
            return
        
        for i in range(index, len(nodes)):
            node = nodes[i]
            if node in used_nodes:
                continue
            
            for neighbor in G.neighbors(node):
                if neighbor not in used_nodes and neighbor > node:
                    new_pairing = current_pairing + [(node, neighbor)]
                    new_used_nodes = used_nodes | {node, neighbor}
                    backtrack(i + 1, new_pairing, new_used_nodes)
    
    backtrack(0, [], set())
    return set(all_pairings)

# Create the graph
G = create_dancer_graph()

# Generate all combinations
all_combinations = generate_all_pairings(G)

print(f"Total number of combinations: {len(all_combinations)}")