Bug Byte
I recently came across this fantastic puzzle Bug Byte devised by the folks at Jane Street from Numberphile.
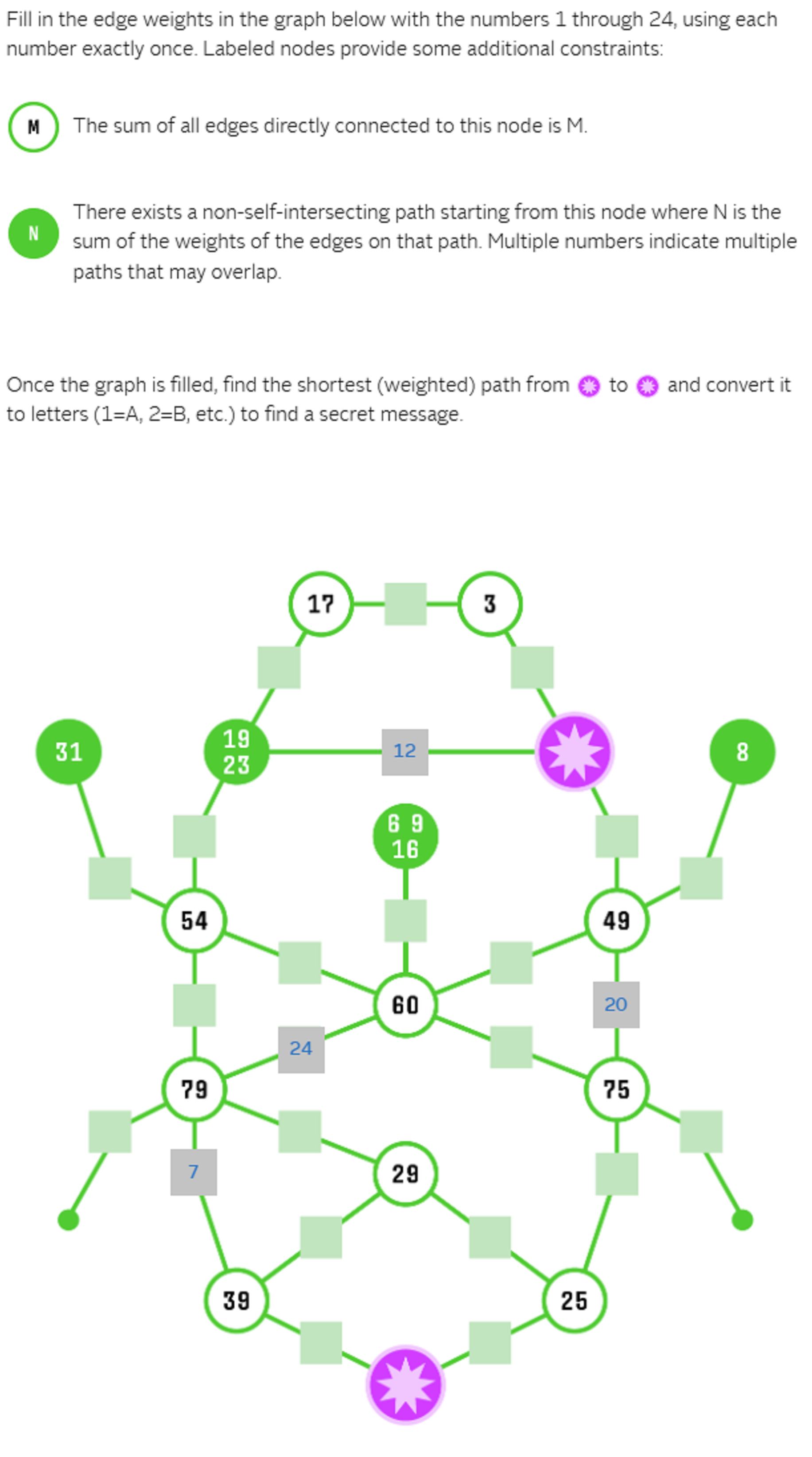
Solution
Jane Street puzzles have a reputation for being fiendishly difficult so I didn’t want to tackle them by hand. I wanted to squash this recreational “bug” using heavy duty computational machinery 😀. Given that this is a puzzle involving Graph Theory and Constraint Programming, I immediately got to work using my favourite Python libraries in this space, networkx and the venerable z3.
First constraint
There are edges in the graph and each edge has to have a distinct weight between and . As the weights of edges have already been provided, we only need variables for the weights of the remaining edges. The code below shows how the above constraint can be implemented using z3.
w = [Int("w%d" % i) for i in range(20)]
s = Solver()
s.add(Distinct(w))
for i in range(20):
s.add(And(w[i] >= 1, w[i] <= 24))
Second constraint
The sum of edges directly connected to white nodes with a green border is equal to the number inside the node. Once we assign the weight variables to each of the edges, the code below shows how to implement this straightforward constraint in z3.
s.add(w[0] + w[1] == 17)
s.add(w[0] + w[2] == 3)
s.add(w[3] + w[4] + w[6] + w[7] == 54)
s.add(24 + w[7] + w[8] + w[9] + w[13] == 60)
s.add(w[5] + w[9] + w[10] + 20 == 49)
s.add(w[13] + w[14] + w[15] + 20 == 75)
s.add(w[11] + w[6] + w[12] + 7 + 24 == 79)
s.add(w[12] + w[16] + w[17] == 29)
s.add(w[14] + w[17] + w[19] == 25)
s.add(7 + w[16] + w[18] == 39)
Third constraint
For each green node, the number inside the node represents the sum of the edge weights of a simple non intersecting path starting from that node. This is the trickiest constraint of the three but thankfully we can get networkx to do the heavy lifting.
Graph Creation
We first create a weighted graph using the code below.
G = nx.Graph()
G.add_edge(1, 2, weight=w[0])
G.add_edge(1, 4, weight=w[1])
G.add_edge(2, 5, weight=w[2])
G.add_edge(4, 5, weight=12)
G.add_edge(4, 7, weight=w[4])
G.add_edge(3, 7, weight=w[3])
G.add_edge(5, 9, weight=w[5])
G.add_edge(6, 9, weight=w[10])
G.add_edge(7, 11, weight=w[7])
G.add_edge(8, 11, weight=w[8])
G.add_edge(9, 11, weight=w[9])
G.add_edge(7, 10, weight=w[6])
G.add_edge(10, 18, weight=w[11])
G.add_edge(10, 14, weight=7)
G.add_edge(10, 13, weight=w[12])
G.add_edge(11, 10, weight=24)
G.add_edge(11, 12, weight=w[13])
G.add_edge(9, 12, weight=20)
G.add_edge(13, 14, weight=w[16])
G.add_edge(12, 16, weight=w[14])
G.add_edge(12, 17, weight=w[15])
G.add_edge(13, 16, weight=w[17])
G.add_edge(14, 15, weight=w[18])
G.add_edge(16, 15, weight=w[19])
Implementing path constraints
From each green node, we find all the simple paths to all other nodes using the all_simple_paths function from networkx and calculate the weight of each path in terms of the weight variables. The thing here to note is that we have to use an “Or” constraint as the number inside each green node has to match the total path weight for one of the paths. The other insight is that the above logic doesn’t change whether there there is one number or multiple numbers in each green node. These insights lead to the simple and elegant code below.
for start_node, total in [(3, 31), (6, 8), (4, 19), (4, 23), (8, 6), (8, 9), (8, 16)]:
constraints = []
for node in set(range(1, 19)) - set([start_node]):
for path in nx.all_simple_paths(G, start_node, node):
constraints.append(nx.path_weight(G, path, weight="weight") == total)
s.add(Or(constraints))
Checking the model for satisfiability
The last part involves checking the model for satisfiability, finding the shortest path between the two nodes containing the stars, mapping the edge weights in the shortest path to alphabets. The code to do that is given below.
if s.check() == sat:
m = s.model()
for u, v in G.edges():
if not (isinstance(G[u][v]["weight"], int)):
G[u][v]["weight"] = m.evaluate(G[u][v]["weight"]).as_long()
sp = list(nx.shortest_path(G, 5, 15, weight="weight"))
for u, v in zip(sp, sp[1:]):
print(chr(ord("@") + G[u][v]["weight"]))
== Python code Putting all the above code together, you will see that the answer is LINKED.
from z3 import Int, Distinct, And, Or, Solver
import networkx as nx
w = [Int("w%d" % i) for i in range(20)]
s = Solver()
s.add(Distinct(w))
for i in range(20):
s.add(And(w[i] >= 1, w[i] <= 24))
s.add(w[0] + w[1] == 17)
s.add(w[0] + w[2] == 3)
s.add(w[3] + w[4] + w[6] + w[7] == 54)
s.add(24 + w[7] + w[8] + w[9] + w[13] == 60)
s.add(w[5] + w[9] + w[10] + 20 == 49)
s.add(w[13] + w[14] + w[15] + 20 == 75)
s.add(w[11] + w[6] + w[12] + 7 + 24 == 79)
s.add(w[12] + w[16] + w[17] == 29)
s.add(w[14] + w[17] + w[19] == 25)
s.add(7 + w[16] + w[18] == 39)
G = nx.Graph()
G.add_edge(1, 2, weight=w[0])
G.add_edge(1, 4, weight=w[1])
G.add_edge(2, 5, weight=w[2])
G.add_edge(4, 5, weight=12)
G.add_edge(4, 7, weight=w[4])
G.add_edge(3, 7, weight=w[3])
G.add_edge(5, 9, weight=w[5])
G.add_edge(6, 9, weight=w[10])
G.add_edge(7, 11, weight=w[7])
G.add_edge(8, 11, weight=w[8])
G.add_edge(9, 11, weight=w[9])
G.add_edge(7, 10, weight=w[6])
G.add_edge(10, 18, weight=w[11])
G.add_edge(10, 14, weight=7)
G.add_edge(10, 13, weight=w[12])
G.add_edge(11, 10, weight=24)
G.add_edge(11, 12, weight=w[13])
G.add_edge(9, 12, weight=20)
G.add_edge(13, 14, weight=w[16])
G.add_edge(12, 16, weight=w[14])
G.add_edge(12, 17, weight=w[15])
G.add_edge(13, 16, weight=w[17])
G.add_edge(14, 15, weight=w[18])
G.add_edge(16, 15, weight=w[19])
for start_node, total in [(3, 31), (6, 8), (4, 19), (4, 23), (8, 6), (8, 9), (8, 16)]:
constraints = []
for node in set(range(1, 19)) - set([start_node]):
for path in nx.all_simple_paths(G, start_node, node):
constraints.append(nx.path_weight(G, path, weight="weight") == total)
s.add(Or(constraints))
if s.check() == sat:
m = s.model()
for u, v in G.edges():
if not (isinstance(G[u][v]["weight"], int)):
G[u][v]["weight"] = m.evaluate(G[u][v]["weight"]).as_long()
sp = list(nx.shortest_path(G, 5, 15, weight="weight"))
for u, v in zip(sp, sp[1:]):
print(chr(ord("@") + G[u][v]["weight"]))