Problem
An ordinary die is rolled until the running total of the rolls first exceeds . What is the most likely final total that will be obtained?
Solution 1
The first solution approach is quite straightforward. We just use Monte Carlo simulation to estimate the required probability.
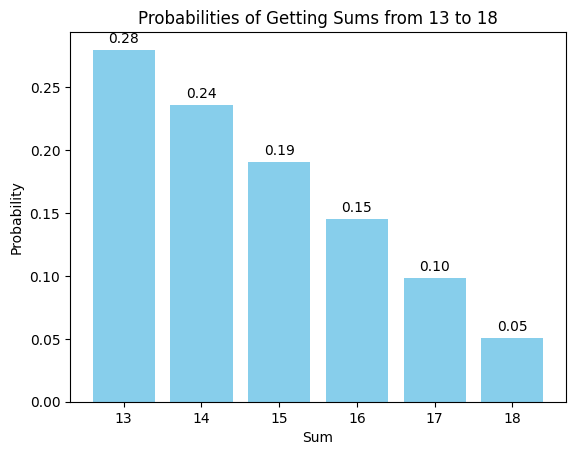
From the graph below we can see that the final total is most likely to be with a probability of .
import numpy as np
import matplotlib.pyplot as plt
def monte_carlo_simulation(n=100000):
results = []
for _ in range(n):
sum_ = 0
while sum_ <= 12:
sum_ += np.random.randint(1, 7) # Roll a die
results.append(sum_)
return results
def calculate_probabilities(results):
probabilities = {i: results.count(i) / len(results) for i in range(13, 19)}
return probabilities
def plot_probabilities(probabilities):
labels = probabilities.keys()
values = probabilities.values()
fig, ax = plt.subplots()
bars = ax.bar(labels, values, color='skyblue')
ax.set_xlabel('Sum')
ax.set_ylabel('Probability')
ax.set_title('Probabilities of Getting Sums from 13 to 18')
for bar in bars:
height = bar.get_height()
ax.annotate(f'{height:.2f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
plt.show()
n_simulations = 100000
results = monte_carlo_simulation(n=n_simulations)
probabilities = calculate_probabilities(results)
plot_probabilities(probabilities)
Solution 2
The second approach is much more interesting. We can count the number of ways of arriving at a total between and such that every number involved in the sum is less than or equal to six and the running total till the second last number is less than or equal to . E.g. is a valid way to reach but not because once you have you have exceed already. We make use of the concept of partitions (a partition of a non-negative integer , also called an integer partition, is a way of writing as a sum of positive integers). If we denote by the partition of where each number of the partition does not exceed , then the number of ways of reaching numbers to is given in the table below:
| Total | Count |
|---|---|
| 13 | p(13,6) |
| 14 | p(8,6) + p(9,6) + p(10,6) + p(11,6) + p(12,6) |
| 15 | p(9,6) + p(10,6) + p(11,6) + p(12,6) |
| 16 | p(10,6) + p(11,6) + p(12,6) |
| 17 | p(11,6) + p(12,6) |
| 18 | p(12,6) |
From the table it is easy to see that the probability of reaching is higher than the probability of reaching the numbers to . We need to compare with to confirm whether or is more likely. Using the code below we see that probability of reaching is and is .
def generate_partitions(number, max_part=6):
def recurse(target, max_part, current_partition):
# Base case: when the target number is 0, yield the current partition
if target == 0:
yield list(current_partition)
else:
# Start from the last part used or max_part, whichever is smaller
start = min(max_part, target)
for next_part in range(start, 0, -1):
# Append next part and recurse
yield from recurse(target - next_part, next_part, current_partition + [next_part])
return list(recurse(number, max_part, []))
def calculate_probability(number):
from collections import Counter
from math import factorial
def partition_probability(partition):
counter = Counter(partition)
l = len(partition)
num = factorial(l)
for _,cnt in counter.items():
num = num * 1/factorial(cnt)
return num/6**l
partitions = generate_partitions(number)
total_probability = sum(partition_probability(p) for p in partitions)
return round(total_probability, 2)
print(f"Total probability for 13:", calculate_probability(13))
prob = 0
for n in range(8,13):
prob += calculate_probability(n)/6
print(f"Total probability for 14:", prob)