Some Off Square

Problem

A circle is randomly generated by sampling two points uniformly and independently from the interior of a square and using these points to determine its diameter. What is the probability that the circle has a part of it that is off the square? Give your answer in exact terms.

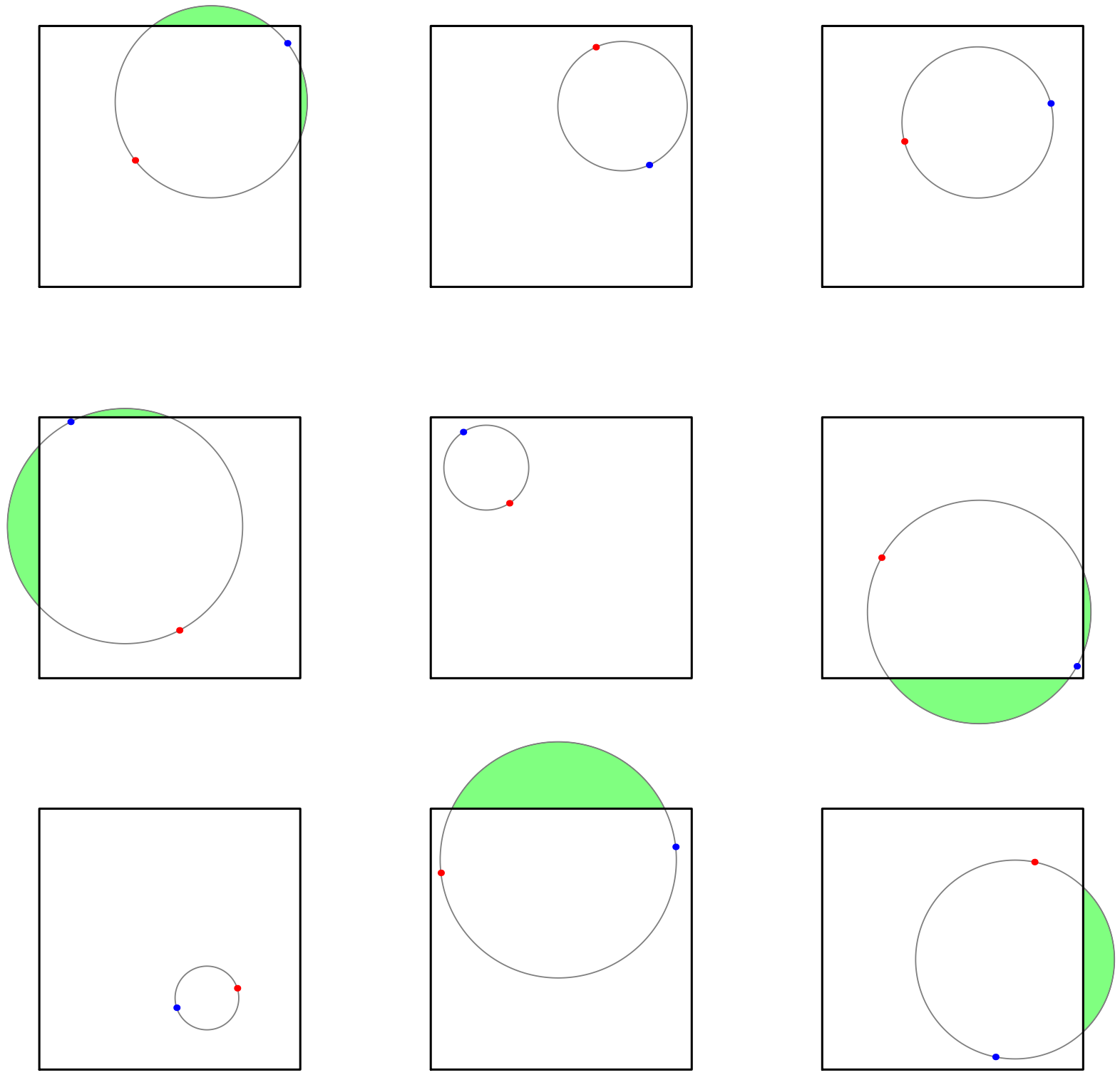
Solution

Let $P_1,P_2$ be the picked points and $M$ be the midpoint of $P_1 P_2$. Our random circle intersects the square iff the distance of $M$ from the boundary of the square is less than the length of $MP_1$ or $MP_2$. Thus, assuming that the square is given by $[−1,1]^2$ and $P_1=(x_1,y_1)$, $P_2=(x_2,y_)$, we want the probability of the event

with $x_1, x_2, y_1, y_2$ being independent and uniformly distributed random variables over the interval $[-1,1]$.

Computational Method

We use Monte Carlo simulation to estimate the probability. Using the Python code below, we see that the required probability is $\mathbf{0.476}$.

from random import uniform
from math import sqrt

runs = 10000000
cnt = 0
for _ in range(runs):
    x_1, x_2, y_1, y_2 = uniform(-1,1), uniform(-1,1), uniform(-1,1), uniform(-1,1)
    if min(2-abs(x_1+x_2), 2-abs(y_1+y_2))<= sqrt((x_1-x_2)**2+(y_1-y_2)**2):
        cnt += 1
print(cnt/runs)