Problem 1
You’re on the north shore of a river, and want to cross to the south, via a series of 13 bridges and six islands, which you can see in the diagram below. But, as you approach the water, night falls, a bad storm rolls in, and you’re forced to wait until morning to try to cross. Overnight, the storm could render some of the bridges unusable — it has a 50 percent chance of knocking out each of the bridges. (The chance is independent for each bridge.) 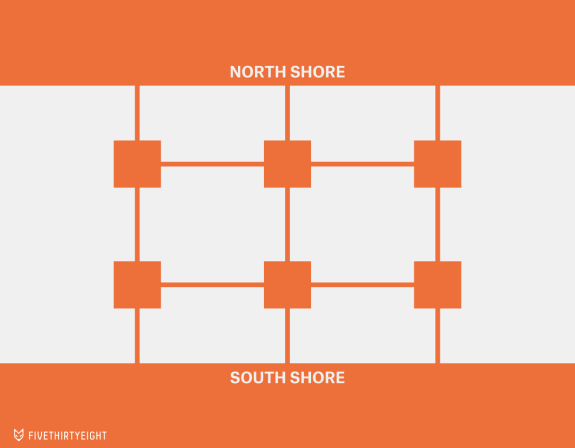
What’s the probability you will be able to cross the river in the morning? (You have no boat, can’t swim, can’t fix the bridges, etc. No tricks.)
Solution 1
from collections import defaultdict
from random import random
def find_path(graph, start, end, path=[]):
path = path + [start]
if start == end:
return path
if start not in graph.keys():
return None
for node in graph[start]:
if node not in path:
newpath = find_path(graph, node, end, path)
if newpath: return newpath
return None
def create_graph(bridges):
graph = defaultdict(list)
for (n1, n2) in bridges:
graph[n1].append(n2)
graph[n2].append(n1)
return graph
runs = 100000
bridges = [(0,1), (0,2), (0,3), (1,2),
(1,4), (2,3), (2,5), (3,6),
(4,5), (4,7), (5,6), (6,7), (7,5)]
knock_out_prob = 0.5
cnt_success = 0
for _ in range(runs):
remaining_bridges = []
for bridge in bridges:
if random() <= knock_out_prob:
remaining_bridges.append(bridge)
if find_path(create_graph(remaining_bridges), 0, 7):
cnt_success += 1
print(cnt_success/runs)The probability that you will be able to cross the river in the morning is 0.5.