Riddler Classic
Congratulations, you’ve made it to the finals of the Riddler Ski Federation’s winter championship! There’s just one opponent left to beat, and then the gold medal will be yours.
Each of you will complete two runs down the mountain, and the times of your runs will be added together. Whoever skis in the least overall time is the winner. Also, this being the Riddler Ski Federation, you have been presented detailed data on both you and your opponent. You are evenly matched, and both have the same normal probability distribution of finishing times for each run. And for both of you, your time on the first run is completely independent of your time on the second run.
For the first runs, your opponent goes first. Then, it’s your turn. As you cross the finish line, your coach excitedly signals to you that you were faster than your opponent. Without knowing either exact time, what’s the probability that you will still be ahead after the second run and earn your gold medal?
Extra credit: Over in the snowboarding championship, there are 30 finalists, including you (apparently, you’re a dual-sport threat!). Again, you are the last one to complete the first run, and your coach signals that you are in the lead. What is the probability that you’ll win gold in snowboarding?
Solution
Let the finishing times for the two rounds of the two players be denoted by \(A_1, A_2, B_1\) and \(B_2\) which are independent and identically distributed normal random variables. We are given that \(B_1 < A_1\). For player \(B\) to win the gold medal, \(A_1 + A_2 > B_1 + B_2\). If we define two new random variables \(X = A_1 - B_1\) and \(Y= A_2 - B_2\), the required probability is given by \(\mathbb{P}[X+Y>0| X >0]\). As \(A_1, A_2, B_1\) and \(B_2\) are independent identically distributed normal random variables, \(X\) and \(Y\) are also independent normal random variables with mean \(0\). The joint probability density function of \(X\) and \(Y\), is symmetric in \(x\) and \(y\). The probability \(\mathbb{P}[X>0 \land X+Y>0]\) can be obtained by integrating the joint density function over the darker region in the figure below: 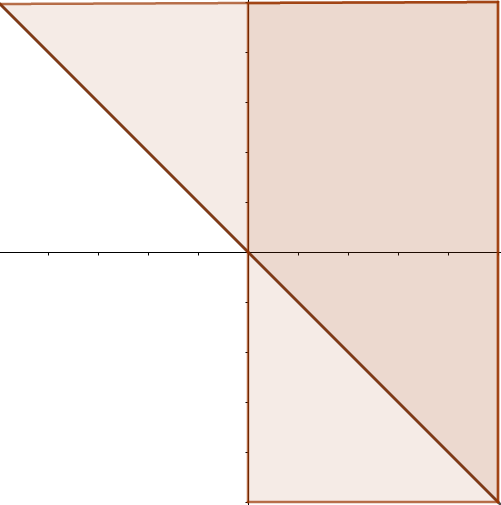 Using the symmetry of the joint density function, it is easy to see that the probability is \(\frac{3}{8}\).
Using the symmetry of the joint density function, it is easy to see that the probability is \(\frac{3}{8}\).
Therefore, the required probability is given by
\[ \begin{align*} \mathbb{P}[X+Y>0| X >0] &= \frac{\mathbb{P}[X>0 \land X+Y>0]}{\mathbb{P}[X>0]} \\ &= \frac{\frac{3}{8}}{\frac{1}{2}} = \frac{3}{4}. \end{align*} \]
The above value matches with that obtained by simulation using the code below. When you have \(30\) players the probability of you winning the gold given that you finished with the lowest time in the first run is \(.31\).
Computational Solution
from numpy.random import normal
runs = 1000000
def prob_gold(n):
num, den = 0, 0
for _ in range(runs):
firstrun_times = normal(0,1,n)
total_times = firstrun_times + normal(0,1,n)
if min(firstrun_times) == firstrun_times[n-1]:
den += 1
if min(total_times) == total_times[n-1]:
num += 1
return num/den
print("Probability of gold when number of players=%i is %f" % (2, prob_gold(2)))
print("Probability of gold when number of players=%i is %f" % (30, prob_gold(30)))