Riddler Express
Area puzzle 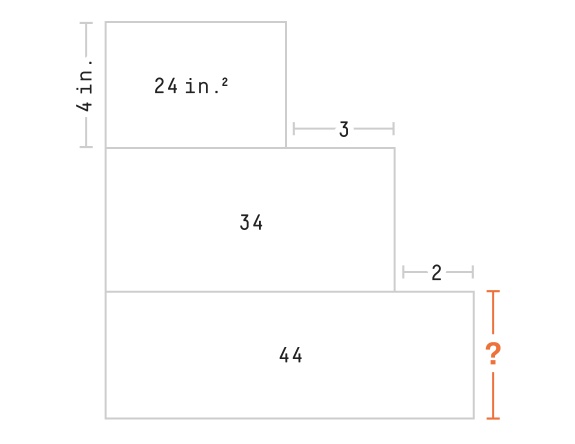
Solution
The length of the top rectangle = \(24/4 = 6 \ in\).
The length of the bottom rectangle = \(6+3+2=11 \ in\).
The height of the bottom rectangle = \(44/11 = 4 \ in\)
Riddler Classic
Area puzzle 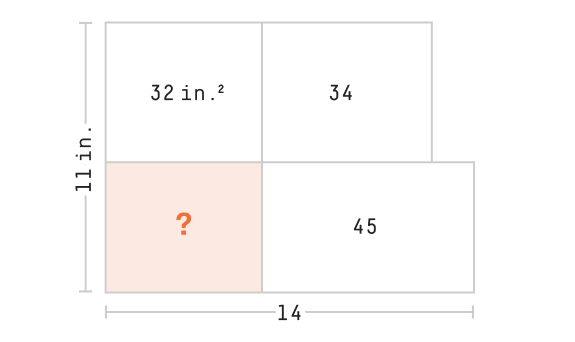
Solution
Let \(x in\) and \(y in\) be the length and height of the shaded rectangle.
We have the following constraints:
\[ \begin{eqnarray} (14-x)y &=& 45 \\ (11-y)x &=& 32 \\ \frac{66}{11-y} &<& 14 \implies y < \frac{44}{7} \end{eqnarray} \]
Subtracting (2) from (1) we have \(14y - 11x = 13\).
Substituting \(y = \frac{13 + 11x}{14}\) in (1), we have
\[ \begin{eqnarray*} 13 + 11x - 13x/14 - 11x^2/14 &=& 45 \\ \implies 11x^2 - 141x + 448 &=& 0 \\ \implies x &=& \frac{141 \pm \sqrt{141^2 - 4 \cdot 11 \cdot 448}}{2 \cdot 11} \\ \implies x = 7 \ and \ y = \frac{45}{7} \ &or& \ x = \frac{64}{11}\ and \ y = \frac{11}{2} \end{eqnarray*} \]
The first solution has to be discarded because of constraint (3).
The area of the shaded region is \(xy = \frac{64}{11} \frac{11}{2} = 32 \ in.^2\)