Riddler Classic
The famous four-color theorem states, essentially, that you can color in the regions of any map using at most four colors in such a way that no neighboring regions share a color. A computer-based proof of the theorem was offered in 1976.
Some 2,200 years earlier, the legendary Greek mathematician Archimedes described something called an Ostomachion. It’s a group of pieces, similar to tangrams, that divides a 12-by-12 square into 14 regions. The object is to rearrange the pieces into interesting shapes, such as a Tyrannosaurus rex. It’s often called the oldest known mathematical puzzle.
Your challenge today: Color in the regions of the Ostomachion square with four colors such that each color shades an equal area. (That is, each color needs to shade 36 square units.) 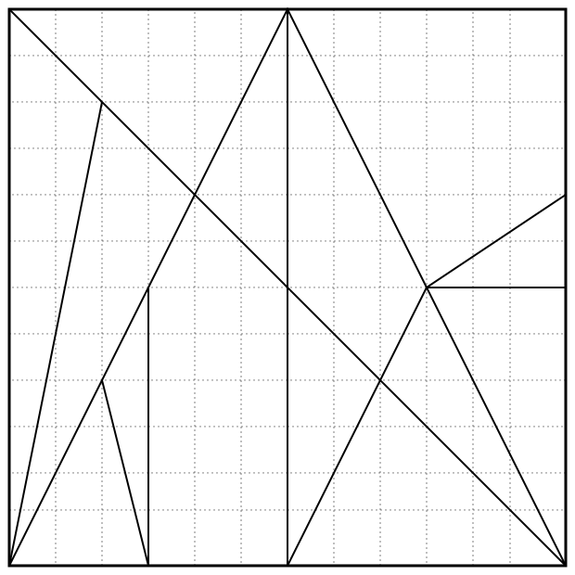
Extra credit: How many solutions to this challenge are there?
Solution
Let the areas be labelled as follows: 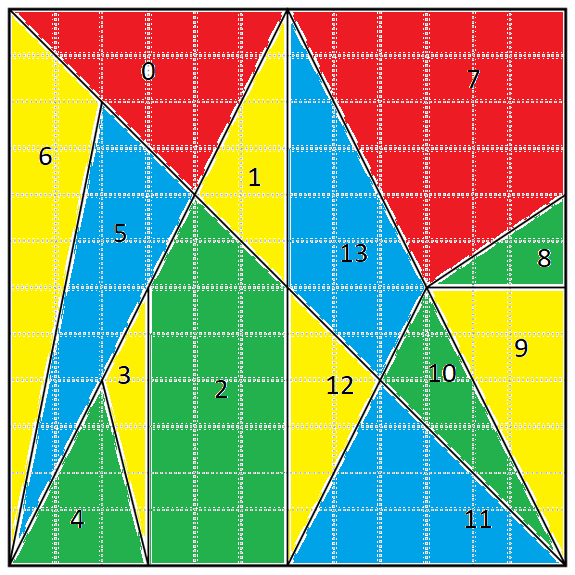
from z3 import *
from math import factorial
connections = {
0:[1,5,6], 1:[0,2,13], 2:[1,12,3,5], 3:[2,4,5],
4:[3,5], 5:[0,2,3,4,6], 6:[0,5], 7:[8,13], 8:[7,9],
9:[8,10], 10:[9,11,13], 11:[10,12], 12:[11,13,2], 13:[1,7,10,12]
}
areas = {
0:12, 1:6, 2:21, 3:3, 4:6, 5:12, 6:12,
7:24, 8:3, 9:9, 10:6, 11:12, 12:6, 13:12
}
col_map = {0:"Red", 1:"Blue", 2:"Green", 3:"Yellow", 4:"Orange", 5:"Pink"}
num_colours = 4
total_area = 144
def OstomachionSolver():
X = [Int("x_%s" % i) for i in range(14)]
s = Solver()
s.add([And(0 <= X[i], X[i]<= num_colours-1) for i in range(14)])
for c in range(num_colours):
s.add(sum([If(X[i] == c, areas[i], 0) for i in range(14)])
== (total_area//num_colours))
for i in range(14):
for j in connections[i]:
s.add(X[i] != X[j])
cnt_sol = 0
while s.check() == sat:
cnt_sol += 1
m = s.model()
s.add(Or([X[i] != m.eval(X[i]) for i in range(14)]))
print("Unique solutions :", cnt_sol / factorial(num_colours))
for i in range(14):
print("Area %d - %s " % (i , col_map[int(str(m.evaluate(X[i])))]))
OstomachionSolver()A colouring which satisfies the constraints is as follows:
Area 0 - Red
Area 1 - Yellow
Area 2 - Green
Area 3 - Yellow
Area 4 - Green
Area 5 - Blue
Area 6 - Yellow
Area 7 - Red
Area 8 - Green
Area 9 - Yellow
Area 10 - Green
Area 11 - Blue
Area 12 - Yellow
Area 13 - Blue