Riddler Express
You have two \(16\)-ounce cups — cup A and cup B. Both cups initially have \(8\) ounces of water in them. You take half of the water in cup A and pour it into cup B. Then, you take half of the water in cup B and pour it back into cup A. You do this again. And again. And again. And then many, many, many more times — always pouring half the contents of A into B, and then half of B back into A. When you finally pause for a breather, what fraction of the total water is in cup A?
Extra credit: Now suppose both cups initially have somewhere between 0 and 8 ounces of water in them. You don’t know the precise amount in each cup, but you know that both cups are not empty. Again, you pour half the water from cup A into cup B, and then half from cup B back to A. You do this many, many times. When you again finally pause for a breather, what fraction of the total water is in cup A?
Computational Solution
The fraction of the total water in Cup A is always \(\bf{\frac{2}{3}}\).
function fracA(a, b)
for i in 1:1000000
a = a/2
b += a
b = b/2
a += b
end
(a, b, a/(a+b))
end
println(fracA(8,8))
println(fracA(8*(1-rand()),8*(1-rand())))Riddler Classic
In Riddler City, all the streets are currently two-way streets. But in an effort to make the metropolis friendlier for pedestrians and cyclists, the mayor has decreed that all streets should be one-way. Meanwhile, the civil engineer overseeing this transition is not particularly invested in the project and will be randomly assigning every block of each street a random direction.
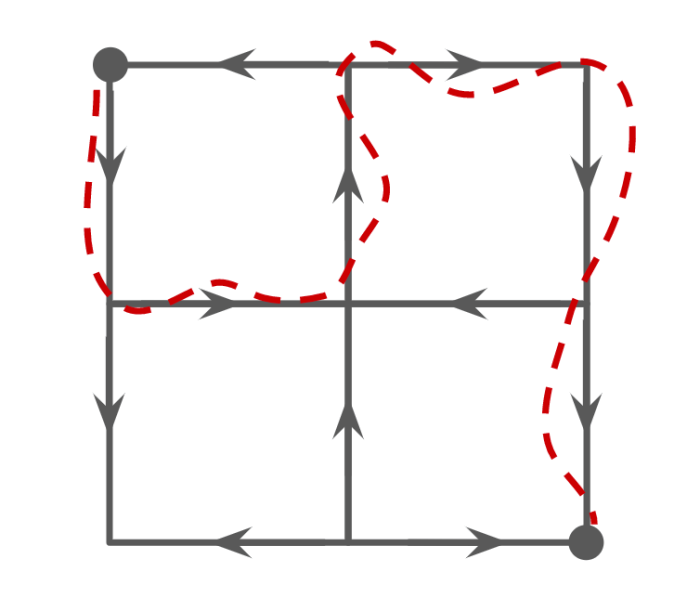
For your daily commute to work, you drive a car two blocks east and two blocks south, as shown in the diagram below. What is the probability that, after each block is randomly assigned a one-way direction, there will still be a way for you to commute to work while staying within this two-by-two block region (i.e., sticking to the \(12\) streets you see in the diagram)? Here is one such arrangement of one-way streets that lets you commute to work:
Computational Solution
The probability that, after each block is randomly assigned a one-way direction, there will still be a way for you to commute to work while staying within this two-by-two block region is \(\bf{0.277}\). The probability of being able to perform a round trip is \(\bf{0.0415}\).
using LightGraphs
import Base.Iterators: product
road_combs = product([(1,2),(2,1)],[(2,3),(3,2)],[(1,4),(4,1)],
[(2,5),(5,2)],[(3,6),(6,3)],[(4,5),(5,4)],
[(5,6),(6,5)],[(4,7),(7,4)],[(7,8),(8,7)],
[(5,8),(8,5)],[(6,9),(9,6)],[(8,9),(9,8)])
cnt, succ, succ_rt = 0, 0, 0
for roads in road_combs
g = SimpleDiGraph(9)
for i in 1:12
add_edge!(g, roads[i][1], roads[i][2])
end
cnt +=1
if has_path(g, 1, 9)
succ += 1
if has_path(g, 9, 1)
succ_rt += 1
end
end
end
println(succ/cnt,"\t", succ_rt/cnt)