Riddler Express
The regular hexagon below has an area of 1. What is the area of the shaded region?
Solution
From the symmetry of the figure, we can see that the quadrilateral is \(\frac{1}{3}^{th}\) the area of the equilateral triangle in which it is embedded. The area of the equilateral triangle is \(\frac{1}{6}^{th}\) of the area of the hexagon. Therefore the area of the shaded quadrilateral is \(\frac{1}{6} \cdot \frac{1}{3} \cdot 1\) = \(\frac{1}{18}\).
Riddler Riddler Classic
The largest circle below has a radius of 10, the medium circle has a radius of 5 and the small, orange circle has a radius of 2. The orange circle crawls counterclockwise along the edge of the largest circle until it meets the medium circle, at which point it crawls up along the edge of the medium circle until it reaches the crest. What is the area of the shaded orange region in the right image? 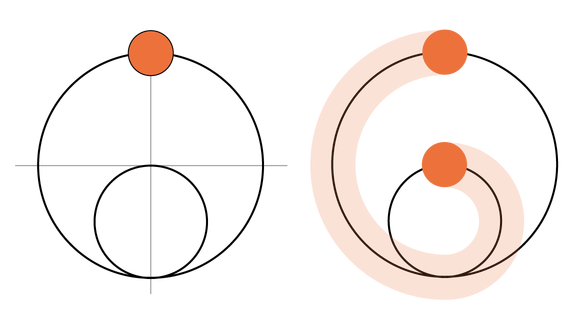
Solution
The area of the shaded orange region has 3 parts.
The area of the small circle given by \(4 \pi\).
The area of the semi annulus with internal radius \(9\) and outer radius \(11\) given by \(\frac{\pi}{2}(12^2 - 8^2)\) = \(40 \pi\).
The area of the semi annulus with internal radius \(4\) and outer radius \(6\) given by \(\frac{\pi}{2}(7^2 - 3^2)\) = $20 $.
Therefore the total area of the shaded region is \(64 \pi\).