Riddler Express
It’s time for a random number duel! You and I will both use random number generators, which should give you random real numbers between \(0\) and \(1\). Whoever’s number is greater wins the duel!
There’s just one problem. I’ve hacked your random number generator. Instead of giving you a random number between \(0\) and \(1\), it gives you a random number between \(0.1\) and \(0.8\).
What are your chances of winning the duel?
Solution
The random generator that I have generates numbers according to \(X \sim \mathcal{U}[a,b]\) where \(0\leq a \leq b\leq1\) and the random generator that you have (in the general case) generates numbers according to \(Y\sim\mathcal{U}[0,1]\). We need the probability, \(\mathbb{P}[X< Y]\). This is given by the area of the trapezium \(EFGH\) divided by the area of the rectangle \(EFIJ\). We have \(|EF| = |IJ| = b-a\), \(|FG|=b\), \(|EH|=a\) and \(|EJ|=1\) in the figure below 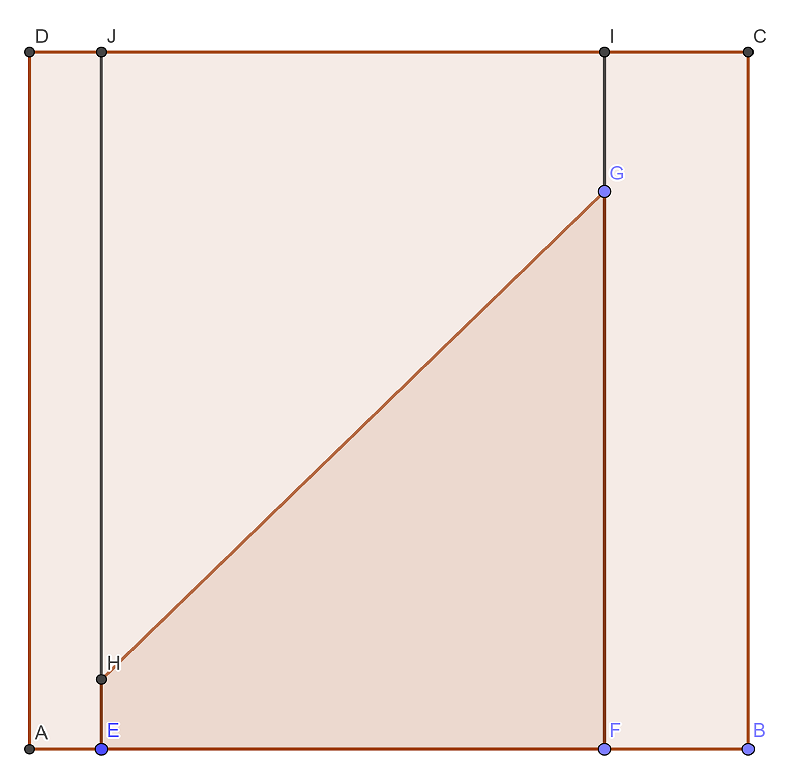
\[ \mathbb{P}[X< Y] = \frac{\frac{1}{2}(b-a)(b+a)}{(b-a)} = \frac{b+a}{2}. \]
In our particular case \(a=0.1\) and \(b=0.8\), therefore the probability of me winning is \(\textbf{0.45}\).
Computational validation
The probability of me winning the duel as per the simulation below is \(\textbf{0.45}\) which validates the result we got earlier.
from numpy.random import uniform
def prob_win(p1l, p1h, p2l, p2h, runs = 1000000):
total_wins = 0
for _ in range(runs):
x, y = uniform(p1l, p1h), uniform(p2l, p2h)
if x > y:
total_wins += 1
return total_wins/runs
print(prob_win(0.1,0.8,0,1))Riddler Classic
I have in my possession 1 million fair coins. Before you ask, these are not legal tender. Among these, I want to find the “luckiest” coin.
I first flip all 1 million coins simultaneously (I’m great at multitasking like that), discarding any coins that come up tails. I flip all the coins that come up heads a second time, and I again discard any of these coins that come up tails. I repeat this process, over and over again. If at any point I am left with one coin, I declare that to be the “luckiest” coin.
But getting to one coin is no sure thing. For example, I might find myself with two coins, flip both of them and have both come up tails. Then I would have zero coins, never having had exactly one coin.
What is the probability that I will — at some point — have exactly one “luckiest” coin?
Solution
Let \(\mathbb{P}[N]\) be the probabillity that we will have exactly one “luckiest” coin starting with \(N\) coins. We have the following recurrence relation:
\[ \begin{align*} \mathbb{P}[N] &= \sum_{i=1}^N \mathbb{P}[i] \frac{N \choose i}{2^N} \\\\ \implies \mathbb{P}[N](1 - \frac{1}{2^N}) &= \sum_{i=1}^{N-1} \mathbb{P}[i] \frac{N \choose i}{2^N} \\\\ \implies \mathbb{P}[N] &= \frac{1}{2^N-1}\sum_{i=1}^{N-1} \mathbb{P}[i] {N \choose i} \\\\ \end{align*} \]
because the probability of ending up with \(i\) heads when you flip \(N\) coins is \(\frac{N \choose i}{2^N}\) and then it is equivalent to starting the game with \(i\) coins. When \(N=1\), \(\mathbb{P}[N]=1\).
Computational Solution
From the code below, we get \(\mathbb{P}[100] \approx \textbf{0.7214}\). Assuming convergence, \(\mathbb{P}[1000000] \approx \textbf{0.7214}\)
from functools import lru_cache
from math import comb
def prob_luckiest_coin(n):
@lru_cache()
def prob(n):
if n == 1:
return 1
else:
total_prob = 0
for i in range(1, n):
total_prob += prob(i)*comb(n,i)
return total_prob/(2**n-1)
return prob(n)
print(prob_luckiest_coin(100))