Express
Inspired by Catriona Shearer (if you don’t know who she is, seriously, check out her puzzles), this week’s Riddler Express is a geometric conundrum: 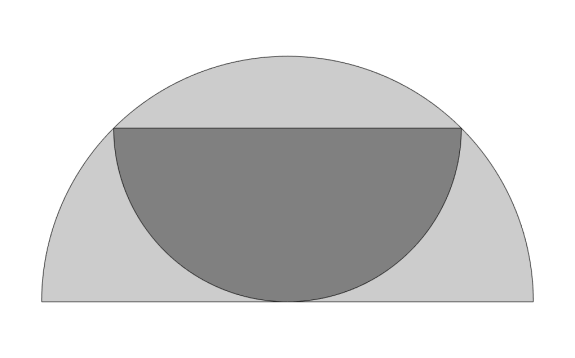
Upside-down semicircle inscribed inside a right side-up semicircle. The smaller semicircle is dark gray, while the larger one is light gray. The picture above shows two semicircles. The lighter region (inside the larger semicircle but outside the smaller one) has an area of 7. What’s the area of the darker region?
Solution
It is easy to see that the radius of the larger semicircle is \(\sqrt{2}\) times the radius of the smaller semi circle. We have
\[ \begin{equation*} \frac{\pi (\sqrt{2}r)^2}{2} - \frac{\pi r^2}{2} = 7 \implies \frac{\pi r^2}{2} = 7 \end{equation*} \]
where \(r\) is the radius of the smaller semi circle.
Therefore, the area of the darker region which is \(\frac{\pi r^2}{2} = \textbf{7}.\)
Classic
You are given a fair, unweighted 10-sided die with sides labeled 0 to 9 and a sheet of paper to record your score. (If the very notion of a fair 10-sided die bothers you, and you need to know what sort of three-dimensional solid it is, then forget it — you have a random number generator that gives you an integer value from 0 to 9 with equal probability. Your loss — the die was a collector’s item.)
To start the game, you roll the die. Your current “score” is the number shown, divided by 10. For example, if you were to roll a 7, then your score would be 0.7. Then, you keep rolling the die over and over again. Each time you roll, if the digit shown by the die is less than or equal to the last digit of your score, then that roll becomes the new last digit of your score. Otherwise you just go ahead and roll again. The game ends when you roll a zero.
For example, suppose you roll the following: 6, 2, 5, 1, 8, 1, 0. After your first roll, your score would be 0.6, After the second, it’s 0.62. You ignore the third roll, since 5 is greater than the current last digit, 2. After the fourth roll, your score is 0.621. You ignore the fifth roll, since 8 is greater than the current last digit, 1. After the sixth roll, your score is 0.6211. And after the seventh roll, the game is over — 0.6211 is your final score.
What will be your average final score in this game?
Solution
from random import choice
def roll():
return choice(range(10))
runs = 1000000
total_score = 0
for _ in range(runs):
rolls = []
while(True):
r = roll()
if r == 0:
break
elif not rolls:
rolls.append(r)
else:
if r <= rolls[-1]:
rolls.append(r)
score = sum([r*10**(-i-1) for i, r in enumerate(rolls)])
total_score += score
print(total_score/runs)The average final score in the game is 0.47360.