Riddler Express
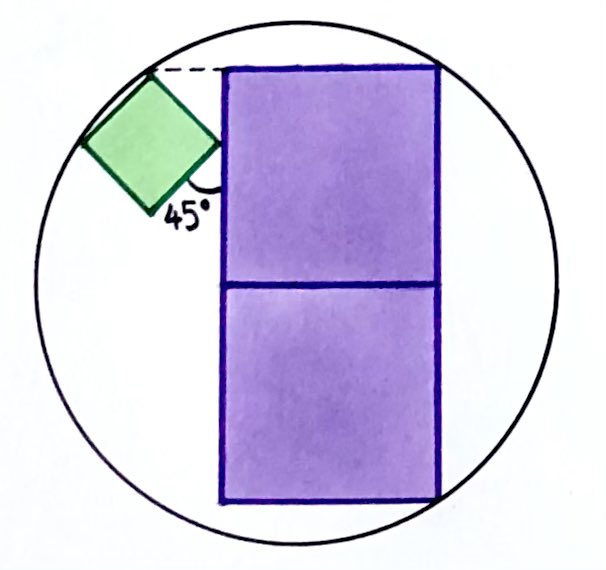
The two larger squares are congruent, and the smaller square makes a \(45\) degree angle with one of the larger squares. Both larger squares touch the circle at one corner, while the smaller square touches the circle at two corners.
How many times greater is the area of one of the larger squares than the area of the smaller square?
Solution
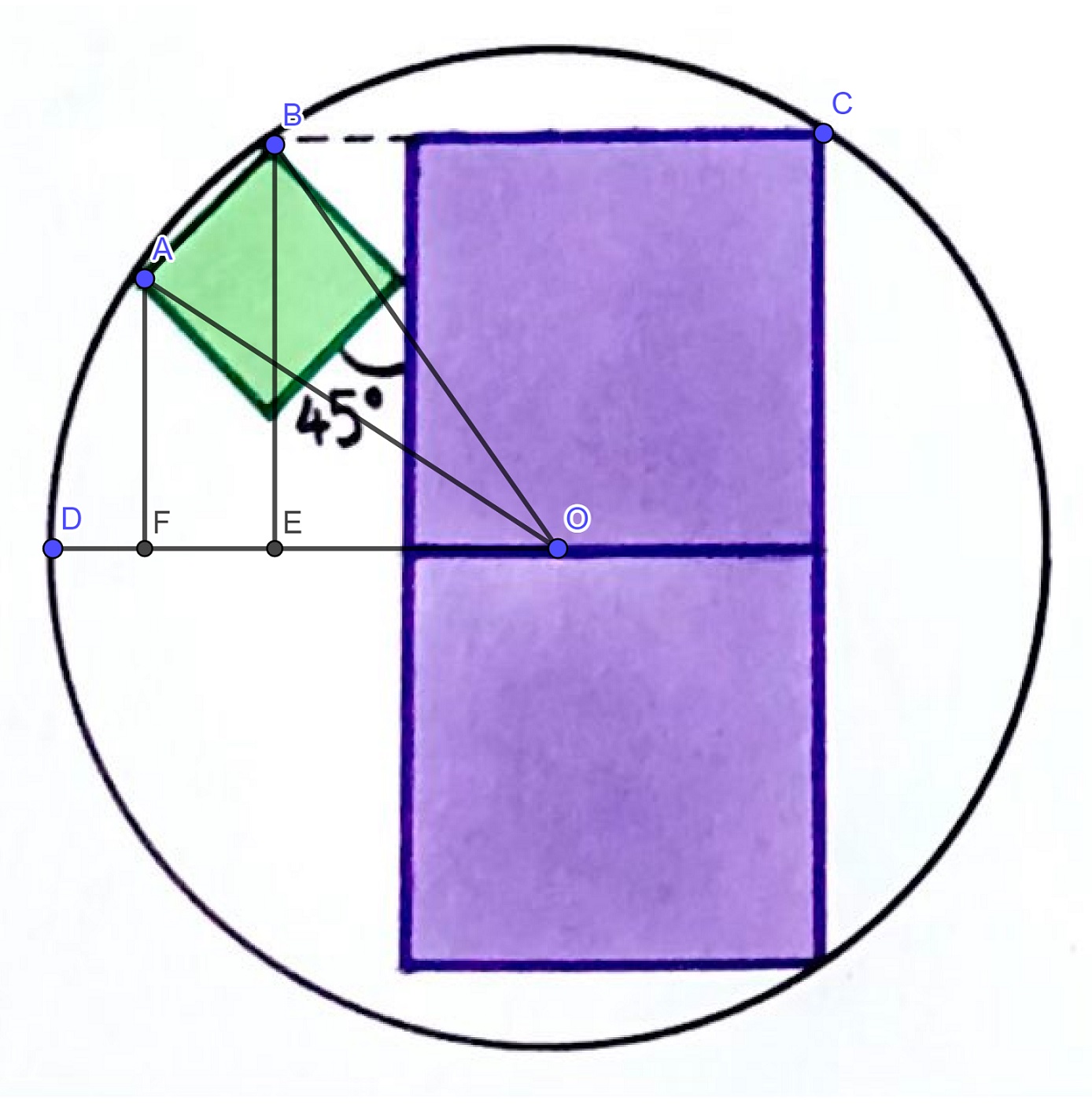
Let \(O\) be the center of the circle, \(x\) be the length of the side of the larger square and \(y\) be the length of the side of the smaller square.
We have the following equations:
\[ OE = BC/2 = \frac{1}{2}(x + \frac{y}{\sqrt{2}})\\\\ BE = x \\\\ AF = BE - \frac{y}{\sqrt{2}}\\\\ OF = OE + \frac{y}{\sqrt{2}} \\\\ OA = OB \\\\ OA^2 = OF^2 + AF^2 \\\\ OB^2 = OE^2 + BE^2 \]
From the above, we have
\[ \begin{align*} -\frac{y^2}{2} + 2 x \frac{y}{\sqrt{2}} &= \frac{y^2}{2} + 2\frac{1}{2}(x + \frac{y}{\sqrt{2}}) \frac{y}{\sqrt{2}} \\\\ \implies \frac{x}{y} &= \frac{3}{\sqrt{2}} \\\\ \implies \frac{x^2}{y^2} &= \frac{9}{2} \end{align*} \]
Riddler Classic
For some perfect squares, when you remove the last digit, you get another perfect square. For example, when you remove the last digit from \(256 (16^2\)), you get \(25 (5^2)\).
The first few squares for which this happens are \(16\), \(49\), \(169\), \(256\) and \(361\). What are the next three squares for which you can remove the last digit and get a different perfect square? How many more can you find?
Extra credit: In the list above, \(169 (13^2)\) is a little different from the other numbers. Not only when you remove the last digit do you get a perfect square, \(16 (4^2)\), but when you remove the last two digits, you again get a perfect square: \(1 (1^2)\). Can you find another square with both of these properties?
Computational Solution
from math import sqrt
cnt = 1
for i in range(20, 1000):
if cnt <= 3 and sqrt(int(str(i*i)[:-1])).is_integer():
print(i*i)
cnt += 1Three more perfect squares that satisfy the conditions of the problem are \(1444, 3249\) and \(18496\).