Riddler Classic
This week’s Classic is being served up by Jordan Ellenberg, whose new book, “Shape,” goes on sale on May \(25\).
One of the many geometers who appears in “Shape” is the great Paul Erdős. In \(1946\), Erdős himself posed a riddle about what are called “isosceles sets”: How many points can you place in d-dimensional space such that any three of them form an isosceles triangle?
In two dimensions, the largest isosceles set has exactly six points, with five forming the vertices of a regular pentagon and the sixth point in the middle. In three dimensions, the largest isosceles set has eight points; in four dimensions, the largest set has \(11\) points. And in dimensions higher than eight, no one knows what the largest isosceles sets might be!
But this week, Jordan is asking about what he calls anti-isosceles sets. Consider a \(N×N\) grid of points. What is the greatest subset of these \(N^2\) points such that no three of them form an isosceles triangle? (Note: Degenerate triangles, or triangles with zero area, do count as triangles here, as long as their three vertices are distinct.)
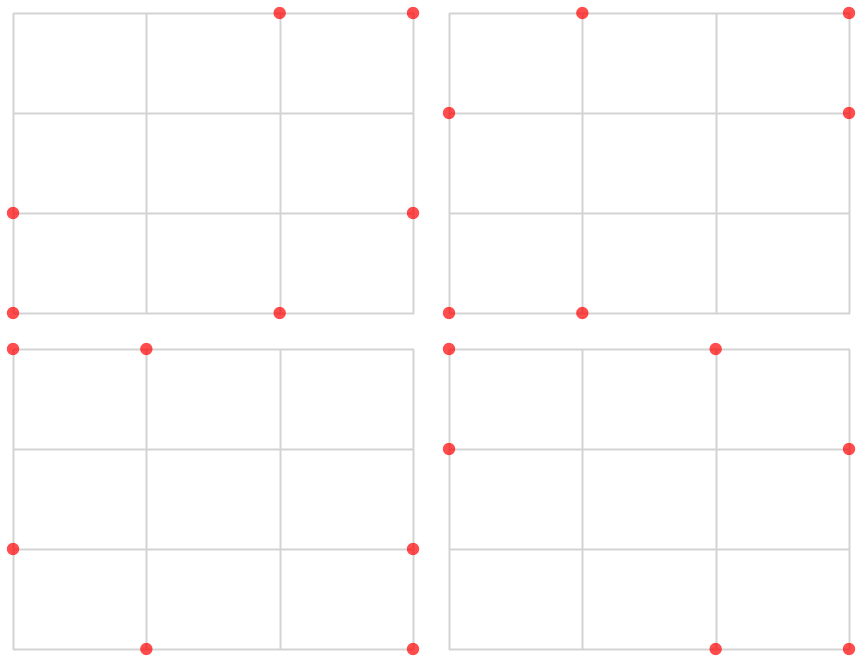
How many points are in the largest anti-isosceles set for a \(4×4\) grid?
Extra credit: What about a \(5×5\) grid, a \(6×6\) grid, or even larger square grids? Can you find an expression (or bounds) for the size of the largest anti-isosceles set for the general \(N×N\) grid? (If you figure out anything about the general case, Jordan would love to hear about it!)
Computational Solution
from itertools import product, combinations
from copy import deepcopy
def isoceles(t):
def d(p1, p2):
return (p1[0]-p2[0])**2 + (p1[1]-p2[1])**2
d1, d2, d3 = d(t[0], t[1]), d(t[1], t[2]), d(t[2], t[0])
if d1 == d2 or d2 == d3 or d3 == d1:
return True
else:
return False
n = 5
grid = product(*[range(n)]*2)
max_size = 6
cur_size = max_size + 1
max_pts_set = []
while True:
cur_size_largest = False
pts_set = []
for pts in combinations(grid, cur_size):
if all([not isoceles(t) for t in combinations(pts, 3)]):
cur_size_largest = True
pts_set.append(pts)
if not cur_size_largest:
break
else:
max_size = cur_size
cur_size += 1
max_pts_set = deepcopy(pts_set)
print(max_size, max_pts_set)Anti-isoceles sets for \(4\times4\) grid
Anti-isoceles sets for \(5\times5\) grid
