Skyscrapers
Fill the grid with numbers, so that every number appears only once in every row and column. The numbers used range from \(1\) upto the length of each row or column.
Imagine the grid is the aerial view of a city block of skyscrapers of varying heights, one within each cell in the grid. Each skyscraper is to be represented as a number indicating its height.A number outside the grid describes how many skyscrapers can be seen along that row or up/down that column from the perspective of that number on the ground. You can only see a skyscraper if smaller skyscrapers are in front of it; you cannot see one if a taller skyscraper is in front of it, blocking the view.
Here is a \(6\times6\) Skyscraper puzzle 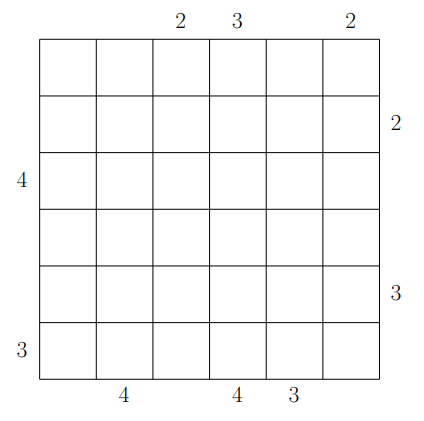
Python code using Z3
from z3 import *
from itertools import permutations
from collections import defaultdict
class SkyscrapersSolver:
def __init__(self, n, puzzle):
self.n = n
self.input = puzzle
self.perms = defaultdict(set)
self.X = [[Int("x_%s_%s" % (i+1, j+1)) for j in range(n)]
for i in range(n)]
self.s = Solver()
self.s.add([And(1 <= self.X[i][j], self.X[i][j]<= n) for i in range(n) for j in range(n)])
for i in range(n):
self.s.add(And(Distinct(self.X[i])))
for j in range(n):
self.s.add(And(Distinct([self.X[i][j] for i in range(n)])))
def classify_permutations(self):
def num_of_visible_ss(arr, reverse=False):
if reverse:
arr = arr[-1::-1]
v = 0
for i in range(0, len(arr)):
if arr[i] >= max(arr[0:i+1]):
v += 1
return v
for p in permutations(range(1, self.n+1)):
self.perms[("R", num_of_visible_ss(p))].add(p)
self.perms[("L", num_of_visible_ss(p, reverse=True))].add(p)
def set_constraints(self):
gl_consts = []
for dr, rn, ns in self.input:
if dr == "R" or dr == "L":
poss_perms = []
for p in self.perms[(dr,ns)]:
poss_perms.append(And([self.X[rn-1][i] == v for i,v in enumerate(p)]))
gl_consts.append(Or(poss_perms))
else:
mdr = "R" if dr == "D" else "L"
poss_perms = []
for p in self.perms[(mdr, ns)]:
poss_perms.append(And([self.X[i][rn-1] == v for i,v in enumerate(p)]))
gl_consts.append(Or(poss_perms))
self.s.add(And(gl_consts))
def output_solution(self):
m = self.s.model()
for i in range(self.n):
print(" ".join(['{:>2}'.format(str(m.evaluate(self.X[i][j])))
for j in range(self.n)]))
def solve(self):
self.classify_permutations()
self.set_constraints()
if self.s.check() == sat:
self.output_solution()
else:
print(self.s)
print("Failed to solve.")
puzzle = ([("R",3,4),("R",6,3),("D",3,2),("D",4,3),("D",6,2),("L",2,2),("L",5,3),
("U",2,4),("U",4,4),("U",5,3)])
sss = SkyscrapersSolver(6, puzzle)
sss.solve()Solution
Here is the solution to the puzzle above
2 6 4 1 3 5
4 3 2 5 6 1
1 2 3 6 5 4
6 5 1 4 2 3
5 4 6 3 1 2
3 1 5 2 4 6