While investigating whether a \(54\) vertex quartic graph has a Hamiltonian cycle in the context of a recreational math problem, I came across this theorem of Tutte, which says that every \(4\)-connected planar graph has a Hamiltonian cycle. I was unsure if a \(54\) vertex quartic graph could be planar, so I googled “graph 54 vertices 108 edges”, lo and behold, here is the beautiful matchstick graph and the Hamiltonian cycle that I found 😊. 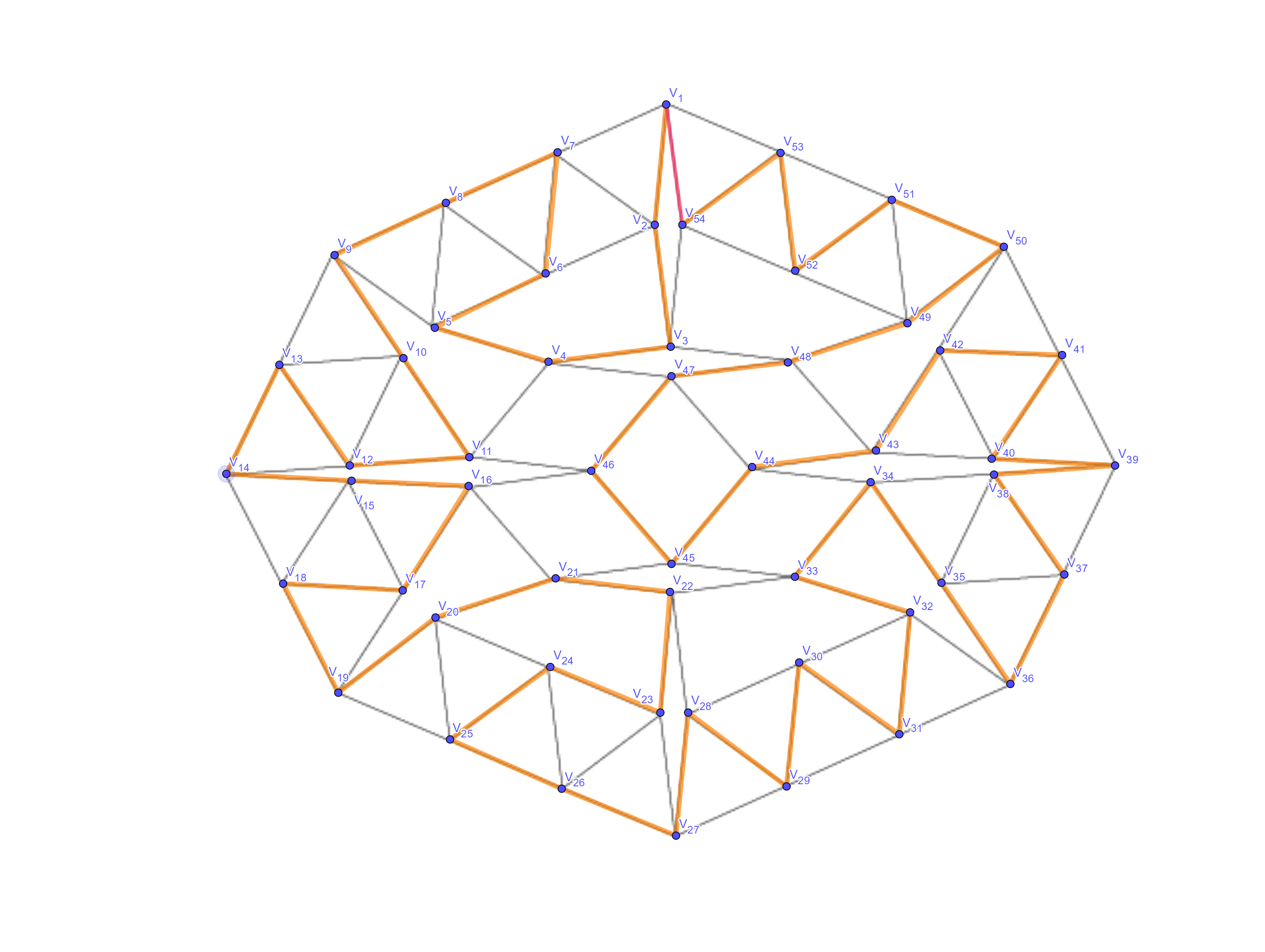
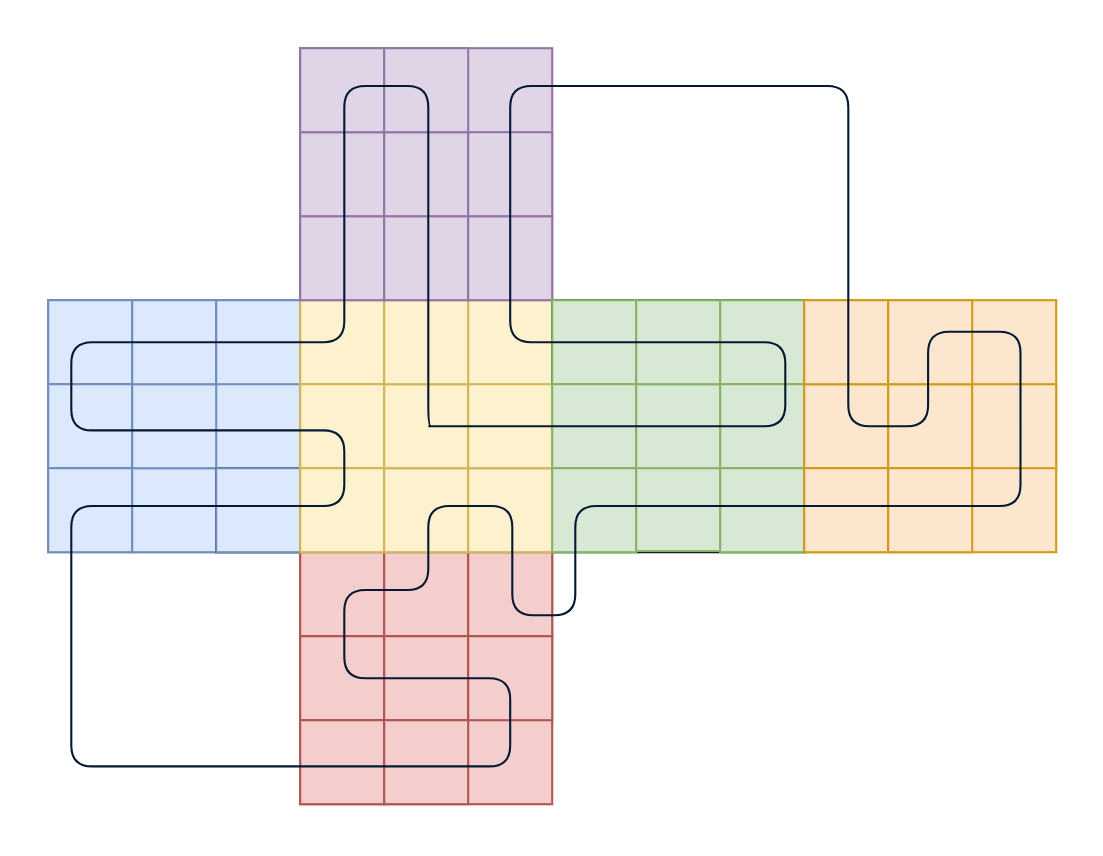
Problem: On the surface of a \(3\times3\) cube is it possible to walk a path starting in one surface square, walking to neighbouring squares, visiting each of the \(54\) squares only once? Is there a circuit?
Solution: Proof without words 😊