Problem
For a regular polygon with \(n\) sides (\(n\) even) and side-length \(2\), prove that the sum of the squares of the segments along a vertical line as in the diagram is \(n\). 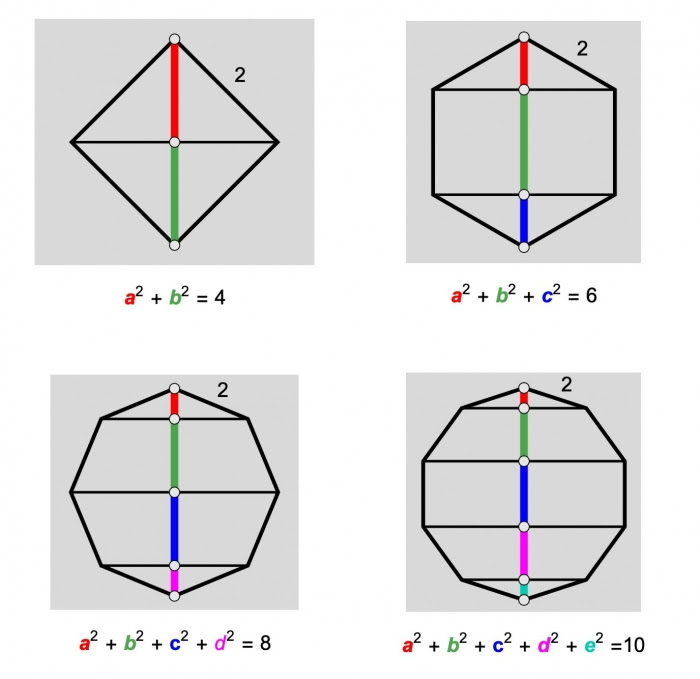 Remarkably, the same identity works for an odd number of sides. But the geometry in the two cases is a little different, so the main problem is for the even case only.
Remarkably, the same identity works for an odd number of sides. But the geometry in the two cases is a little different, so the main problem is for the even case only.
Solution
A regular polygon with \(n\) sides where \(n\) is even has \(n=4k\) or \(n=4k+2\) sides. The coloured line segments are the projections of the polygon sides onto the \(y\) axis.
Case: \(n=4k\)
Let a regular polygon with \(n=4k\) sides and side length \(2\) be oriented such that its center is at the origin and both the \(x\) and \(y\) axis are lines of symmetry.Let the sides of the polygon be numbered from \(1\) to \(4k\) in anti clockwise direction starting from the side with one vertex on the positive \(x\) axis and another vertex in the first quadrant. Let \(x_i\) and \(y_i\) be the lengths of the projections of side \(i\) on the \(x\) and \(y\) axis respectively. We have \(x_i^2+ y_i^2 = 2^2\) for all \(i \in \{1, \dots, 4k\}\). We also have \(x_{i+k} = y_i\) and \(y_{i+k} = x_i\) because the side \(i+k\) is perpendicular to side \(i\) (the angle between them is \(\frac{2\pi}{4k}k\)).
The sum we are interested in is
\[ \sum_{i=k+1}^{3k} y_i^2 = \sum_{i=1}^{2k} y_i^2 \]
due to symmetry.
We also have
\[ \begin{aligned} \sum_{i=1}^{2k} y_i^2 &= \sum_{i=1}^{k} y_i^2 + \sum_{i=k+1}^{2k} y_i^2 \\\\ &= \sum_{i=1}^{k} y_i^2 + \sum_{i=1}^{k} x_i^2 \\\\ &= \sum_{i=1}^{k} x_i^2 + y_i^2 \\\\ & = k \cdot 2^2 = 4k = n \end{aligned} \]
This completes the proof of the formula for the case where the polygon has \(n=4k\) sides.
Case: \(n=4k+2\)
Haven’t been able to find an elegant geometric proof yet 😊. A simple trigonometric proof is given below. It is fairly straightforward 😉 to see that the required sum of squares of projections on the \(y\)-axis is
\[ \begin{aligned} &2 \sum_{i=1}^{k} \left(2 \sin{\frac{(2i-1)\pi}{4k+2}} \right)^2 + 4 \\\\ &= 2\sum_{i=1}^k \left(2 - 2\cos{\frac{(2i-1)\pi}{2k+1}} \right) + 4 \\\\ & = 4k + 4 - 4\sum_{i=1}^{k} \cos{\frac{(2i-1)\pi}{2k+1}} \\\\ & = 4k + 4 - \frac{2}{\sin{\frac{\pi}{2k+1}}} \sum_{i=1}^{k} \sin{\frac{2i\pi}{2k+1}} - \sin{\frac{2(i-1)\pi}{2k+1}}\\\\ & = 4k + 4 - 2 \frac{\sin{\frac{2k\pi}{2k+1}}}{\sin{\frac{\pi}{2k+1}}} \\\\ & = 4k + 2 \end{aligned} \]
This completes the proof of the formula for the case where the polygon has \(n=4k+2\) sides.