Problem
A white knight and a black knight are situated on diagonally opposite corners of a \(3 \times 3\) square. In turn, starting with White, they move randomly until (inevitably) Black captures White. What is the expected number of Black moves to achieve capture?
Solution
Key Observations
- The complete state of the game is determined by the position of the two knights on the board.
- The next state of the game only depends on the current state.
- Multiple configurations(rotations, reflections) of the board can be collapsed into a single state.
This is essentially a Markov Chain problem.
Board States
The diagram below illustrates all possible board states apart from the absorbing state 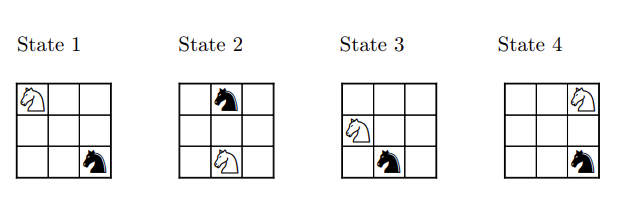
State 1 is the initial state.
State Transition Matrix
The state transition diagram for the game markov chain is shown below 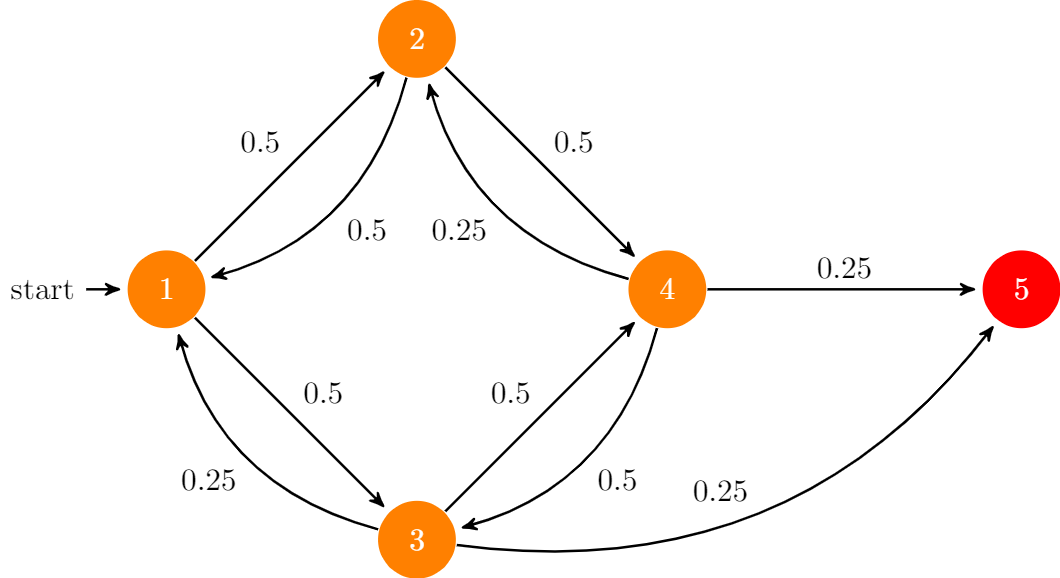
State 5 (where the black knight captures the white knight) is the absorbing state of the markov chain.
The transition matrix \(\mathbf{Q}\) is given by
\[ \mathbf{Q} = \begin{bmatrix} 0 & 0.5 & 0.5 & 0\\ 0.5 & 0 & 0 & 0.5 \\ 0.25 & 0 & 0 &0.5 \\ 0 & 0.25 & 0.5 &0 \end{bmatrix} \]
Fundamental matrix and expectation
For a Markov chain \(\mathbf{P}\), the matrix \(\mathbf{N} = (\mathbf{I} − \mathbf{Q})^{−1}\) is called the fundamental matrix for \(\mathbf{P}\).
Let \(t_i\) be the expected number of steps before the chain is absorbed, given that the chain starts in state \(s_i\), and let \(\mathbf{t}\) be the column vector whose \(i^{th}\) entry is \(t_i\). Then \(\mathbf{t} = \mathbf{Nc}\), where \(\mathbf{c}\) is a column vector all of whose entries are \(1\).
We have
\[ \begin{align*} \mathbf{Nc} &= (\mathbf{I - Q})^{-1}\mathbf{c} \\ &= \begin{bmatrix} 1 & -0.5 & -0.5 & 0\\ -0.5 & 1 & 0 & -0.5 \\ -0.25 & 0 & 1 & -0.5 \\ 0 & -0.25 & -0.5 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 8 \\ 8 \\ 6 \\ 6 \end{bmatrix} \end{align*} \]
Therefore, the expected number of steps taken by the black knight to capture the white knight from the initial configuration is \(\mathbf{8}\).
Computational Verification
from random import choice
transitions = {
(0,0):[(2,1),(1,2)],
(0,1):[(2,0),(2,2)],
(0,2):[(1,0),(2,1)],
(1,0):[(0,2),(2,2)],
(1,2):[(0,0),(2,0)],
(2,0):[(0,1),(1,2)],
(2,1):[(0,0),(0,2)],
(2,2):[(1,0),(0,1)]
}
runs = 100000
tl = 0
for _ in range(runs):
b, w = (0,0), (2,2)
l = 0
while True:
l += 1
w = choice(transitions[w])
b = choice(transitions[b])
if b == w:
break
tl += l
print(tl/runs)