Problem
Consider a 2x12 rectangle with dotted lines marking the 24 squares. How many sets R are there such that R is connected, R is obtained by cutting on the dotted lines, and R contains at least one square at the left end and at least one square at the right end?
“Connected” means that one can get from any square in R to any other by a path of adjacent squares, adjacency meaning that at least one edge is shared. Symmetry is ignored: if R is congruent to R’ but they involve different squares, they count as different. There is in fact a formula for the count for the \(2 \times n\) case (and some extensions to \(m \times n\)). Here is an example of a set R. 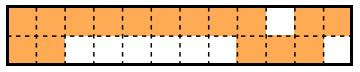
For a \(2 \times 2\) rectangle there are seven such sets, shown below. 
Source: S. Durham and T. Richmond, Connected subsets of an nx2 rectangle, College Math. J., 51, (Jan. 2020), 32-42.
Solution
Let \(A(n)\) be the number of sets as in the problem for 2xn grid. Let \(T(n)\) be the number of sets as in the problem, but that have in the rightmost column a square on the top but not the bottom. Note that this is the same, by symmetry, if we count sets that have a square on the bottom but not the top in the last column. Let \(B(n)\) be the number of sets as in the problem that have the rightmost column contain both squares. Note that \(B(n) = A(n-1)\).
We have \(A(n) = B(n) + 2 L(n)\), so
\[ \begin{equation} \label{eq1} 2 L(n) = A(n) - B(n) = A(n) - A(n - 1) \end{equation} \]
Also \(L(n) = L(n-1) + B(n - 1) = L(n-1) + A(n - 2)\), so
\[ \begin{equation} \label{eq2} 2 L(n) = 2 L(n - 1) + 2 A(n - 2) \end{equation} \]
Now \(\ref{eq1}\) and \(\ref{eq2}\) give,
\[ \begin{align} A(n) - A(n - 1) &=& 2 L(n - 1) + 2 A(n - 2) \nonumber\\\\ &=& A(n - 1) - A(n - 2) + 2 A(n - 2) \nonumber\\\\ \implies A(n) &=& 2 A(n - 1) + A(n - 2) \label{eq3} \end{align} \]
Solving the recurrence relation \(\ref{eq3}\) using the initial conditions \(A(1) = 3\) and \(A(2) = 7\) gives us the sequence \(3, 7, 17, 41,\dots\) for \(A(n)\).
What is interesting about this sequence: \(3, 7, 17, 41, 99, 239, 577,...\) is that it is identical with the numerators of the convergents of the continued fraction of \(\sqrt{2}\):
\(1/1 , 3/2 , 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, \dots, 47321/33461\).
Here is the Python code for calculating \(A(n)\) and generating the connected paths.
def num_connected_paths(n):
if n == 1:
return 3
if n == 2:
return 7
cnt = 2
t_n_2, t_n_1 = 3, 7
while(cnt != n):
t_n_2, t_n_1 = t_n_1, 2*t_n_1 + t_n_2
cnt += 1
return t_n_1
print(num_connected_paths(5))
def connected_paths(n):
if n == 1:
return [[(1,0)],[(0,1)],[(1,1)]]
ext_paths = []
for path in connected_paths(n-1):
s1, s2 = path[-1]
ext_paths.append(path + [(1,1)])
if (s1,s2) == (1,1):
ext_paths.append(path + [(1,0)])
ext_paths.append(path + [(0,1)])
else:
ext_paths.append(path + [(s1,s2)])
return ext_paths
print(len(connected_paths(5)))