Riddler Express
Area puzzle 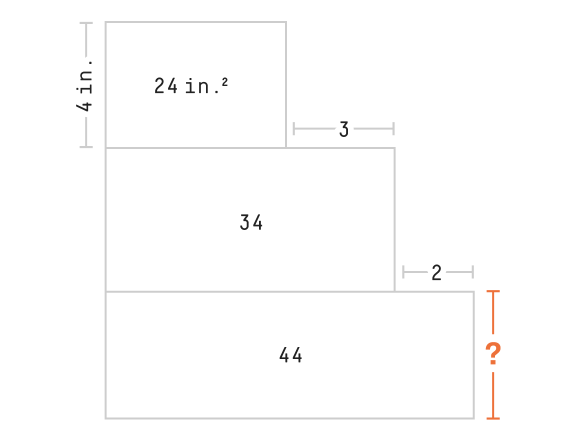
Solution
The length of the top rectangle = 24/4=6 in.
The length of the bottom rectangle = 6+3+2=11 in.
The height of the bottom rectangle = 44/11=4 in
Riddler Classic
Area puzzle 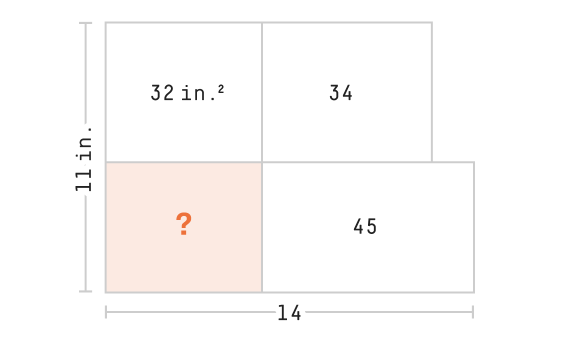
Solution
Let xin and yin be the length and height of the shaded rectangle.
We have the following constraints:
(14−x)y(11−y)x11−y66==<453214⟹y<744
Subtracting (2) from (1) we have 14y−11x=13.
Substituting y=1413+11x in (1), we have
13+11x−13x/14−11x2/14⟹11x2−141x+448⟹x⟹x=7 and y=745 or=45=0=2⋅11141±1412−4⋅11⋅448 x=1164 and y=211
The first solution has to be discarded because of constraint (3).
The area of the shaded region is xy=1164211=32 in.2

