Can You Bake The Radish Pie?

Riddler Express

I recently came across a rather peculiar recipe for something called Babylonian radish pie. Intrigued, I began to follow the directions, which said I could start with any number of cups of flour.

Any number? I mean, I had to start with some flour, so zero cups wasn’t an option. But according to the recipe, any positive value was fair game. Next, I needed a second amount of flour that was 3 divided by my original number. For example, if I had started with two cups of flour, then the recipe told me I now needed $3$ divided by $2$, or $1.5$, cups at this point.

I was then instructed to combine these amounts of flour and discard half. Apparently, this was my new starting amount of flour. I was to repeat the process, combining this amount with $3$ divided by it and then discarding half.

The recipe told me to keep doing this, over and over. Eventually, I’d have the proper number of cups of flour for my radish pie.

How many cups of flour does the recipe ultimately call for?

Solution 1

In the limit after convergence, let $f$ be number of cups of flour required as per the recipe. We have

Solution 2

This involves recognizing the recipe is infact a classic algorithm that is “Newton’s” method to compute square roots $x = \sqrt{a}$ for $a > 0$, i.e. to solve $x^2 = a$. The algorithm involves the following steps:

1. Starts with some guess $x_1 > 0$.

2. Compute the sequence of improved guesses:

In light of the above, it is easy to see that the recipe ultimately calls for $\sqrt{3}$ cups of flour.

Computational Solution

From the code below, we see that the recipe ultimately calls for $\sqrt{3} \approx 1.732$ cups.

def num_cups():
    s, c = 2, 0
    while True:
        c = 0.5*(s + 3/s)
        if abs(s-c) < 0.000001:
            break
        s = c
    return c

print(num_cups())

Riddler Classic

Lately, Rushabh has been thinking about very large regular polygons — that is, a polygon all of whose sides and angles are congruent. His latest construction is a particular regular $1,000$-gon, which has $1,000$ sides of length $2$. Rushabh picks one of its longest diagonals, which connects two opposite vertices.

Now, this $1,000$-gon has many diagonals, but only some are perpendicular to that first diagonal Rushabh picked. If you were to slice the polygon along all these perpendicular diagonals, you’d break the first diagonal into $500$ distinct pieces. Rushabh is curious — what is the product of the lengths of all these pieces?

Extra credit: Now suppose you have a regular $1,001$-gon, each of whose sides has length $2$. You pick a vertex and draw an altitude to the opposite side of the polygon. Again, you slice the polygon along all the perpendicular diagonals, breaking the altitude into $500$ distinct pieces. What’s the product of the lengths of all these pieces this time?

Solution

The segments of the problem are the vertical components of the polygon’s sides on its right half as shown in the diagram below; these lengths are $V_k = 2 \sin\left((2k - 1) \frac{π}{n}\right)$, with $k = 1, 2,…, n/2$ where $n$ is even (here we make use of the fact that the polygon’s side rotates through $2π/n$ as as it moves to the next side).

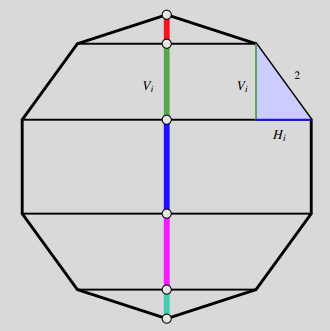
The product of the lengths of all these segments is given by

Let $f(x) = \prod_{k=1}^{n-1} (x - e^{-i2\pi k/n})$. The roots of this polynomial are the non-trivial $n$-th roots of unity, so

Plugging in $1$ for $x$ yields $f(1) = \prod_{k=1}^{n-1} (1 - e^{-i2\pi k/n}) = n$.

Using the above result, we have

Therefore, when $n=1000$, the required product $P = 2e^{in\pi}/i^{n/2}$ has the value $\textbf{2}$.

Extra Credit

For the case when $n$ is odd, we need to calculate the product

We make use of the result below. You can find the proof here.

We have,

When $n=1001$, the required product has the value $\sqrt{1001} \approx \textbf{31.63854}$.