Solving Ostomachion using Z3

Riddler Classic

The famous four-color theorem states, essentially, that you can color in the regions of any map using at most four colors in such a way that no neighboring regions share a color. A computer-based proof of the theorem was offered in 1976.

Some 2,200 years earlier, the legendary Greek mathematician Archimedes described something called an Ostomachion. It’s a group of pieces, similar to tangrams, that divides a 12-by-12 square into 14 regions. The object is to rearrange the pieces into interesting shapes, such as a Tyrannosaurus rex. It’s often called the oldest known mathematical puzzle.

Your challenge today: Color in the regions of the Ostomachion square with four colors such that each color shades an equal area. (That is, each color needs to shade 36 square units.)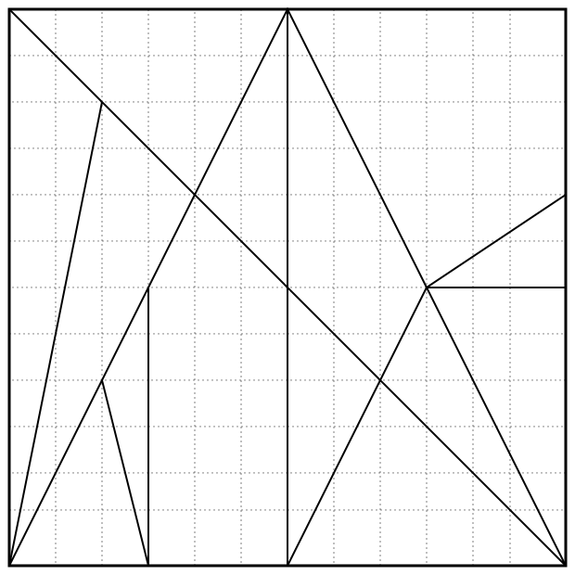

Extra credit: How many solutions to this challenge are there?

Solution

Let the areas be labelled as follows: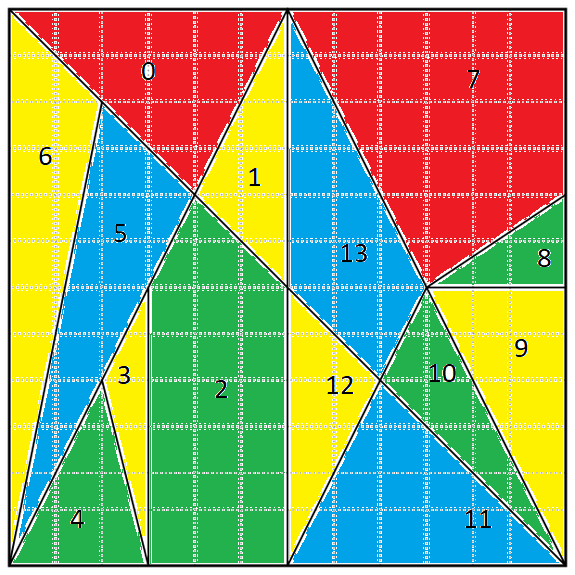

from z3 import *
from math import factorial

connections = { 
    0:[1,5,6], 1:[0,2,13], 2:[1,12,3,5], 3:[2,4,5],
    4:[3,5], 5:[0,2,3,4,6], 6:[0,5], 7:[8,13], 8:[7,9],
    9:[8,10], 10:[9,11,13], 11:[10,12], 12:[11,13,2], 13:[1,7,10,12]
}

areas = { 
    0:12, 1:6, 2:21, 3:3, 4:6, 5:12, 6:12, 
    7:24, 8:3, 9:9, 10:6, 11:12, 12:6, 13:12
}

col_map = {0:"Red", 1:"Blue", 2:"Green", 3:"Yellow", 4:"Orange", 5:"Pink"}

num_colours = 4
total_area = 144
def OstomachionSolver():
    X = [Int("x_%s" % i) for i in range(14)]
    s = Solver()
    s.add([And(0 <= X[i], X[i]<= num_colours-1) for i in range(14)])
    for c in range(num_colours):
        s.add(sum([If(X[i] == c, areas[i], 0) for i in range(14)]) 
                == (total_area//num_colours))
    for i in range(14):
        for j in connections[i]:
            s.add(X[i] != X[j])

    cnt_sol = 0
    while s.check() == sat:
        cnt_sol += 1
        m = s.model()
        s.add(Or([X[i] != m.eval(X[i]) for i in range(14)]))
    print("Unique solutions :", cnt_sol / factorial(num_colours))
    for i in range(14):
        print("Area %d - %s " % (i , col_map[int(str(m.evaluate(X[i])))])) 

OstomachionSolver()

A colouring which satisfies the constraints is as follows:

Area 0 - Red

Area 1 - Yellow

Area 2 - Green

Area 3 - Yellow

Area 4 - Green

Area 5 - Blue

Area 6 - Yellow

Area 7 - Red

Area 8 - Green

Area 9 - Yellow

Area 10 - Green

Area 11 - Blue

Area 12 - Yellow

Area 13 - Blue