Can You Solve This Astronomical Enigma?

Riddler Express

Earlier this year, a new generation of Brood X cicadas had emerged in many parts of the U.S. This particular brood emerges every $17$ years, while some other cicada broods emerge every $13$ years. Both $13$ and $17$ are prime numbers — and relatively prime with one another — which means these broods are rarely in phase with other predators or each other. In fact, cicadas following a $13$-year cycle and cicadas following a $17$-year cycle will only emerge in the same season once every $221$ (i.e., $13$ times $17$) years!

Now, suppose there are two broods of cicadas, with periods of $A$ and $B$ years, that have just emerged in the same season. However, these two broods can also interfere with each other one year after they emerge due to a resulting lack of available food. For example, if $A$ is $5$ and $B$ is $7$, then B’s emergence in year $14$ (i.e., $2$ times $7$) means that when $A$ emerges in year $15$ (i.e., $3$ times $5$) there won’t be enough food to go around.

If both $A$ and $B$ are relatively prime and are both less than or equal to $20$, what is the longest stretch these two broods can go without interfering with one another’s cycle? (Remember, both broods just emerged this year.) For example, if $A$ is $5$ and $B$ is $7$, then the interference would occur in year $15$.

Computational Solution

Using the code below, we see that the longest stretch the two broods can go without interfering with one another’s cycle is $\textbf{153}$.

from math import gcd

def max_non_intf(n):
    def min_non_intf(a,b):
        for x in range(0, a*b+1, a):
            for y in range(0, a*b+1, b):
                if abs(x-y)==1:
                    return max(x,y)
    
    valid_tuples = [(a, b) for a in range(1, n) for b in range(a, n+1)
                    if gcd(a,b) == 1]
    return max([min_non_intf(a,b) for a,b in valid_tuples])

print(max_non_intf(20))

Riddler Classic

The astronomers of Planet Xiddler are back!

This time, they have identified three planets that circularly orbit a neighboring star. Planet $A$ is three astronomical units away from its star and completes its orbit in three years. Planet $B$ is four astronomical units away from the star and completes its orbit in four years. Finally, Planet $C$ is five astronomical units away from the star and completes its orbit in five years. They report their findings to Xiddler’s Grand Minister, along with the auspicious news that all three planets are currently lined up (i.e., they are collinear) with their star. However, the Grand Minister is far more interested in the three planets than the star and wants to know how long it will be until the planets are next aligned.

How many years will it be until the three planets are again collinear (not necessarily including the star)?

Solution

Let $r_1, r_2, r_3$ and $\omega_1, \omega_2, \omega_3$ be the radii and the angular velocities of the three planets. The cartesian coordinates of the planets are $(r_i\cos\omega_it, r_i\sin\omega_it)$ where $i \in \{1,2,3\}$. When the three planets are collinear then

For,

the above determinant reduces to

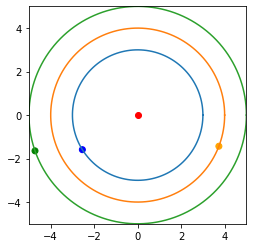
Solving the above equation numerically for $t$, we get the time period until the three planets are collinear next to be $\textbf{7.766}$ years.

The Python code for numerically solving the above equation and plotting the positions of the three planets is given below.

from scipy.optimize import fsolve
from math import sin, cos, pi
import numpy as np
import matplotlib.pyplot as plt

def polToCart(r, w, t):
    return (r*cos(w*t), r*sin(w*t))

def circle(radius):
    angle = np.linspace(0, 2*np.pi, 150) 
    x = radius*np.cos(angle) 
    y = radius*np.sin(angle) 
    return (x,y)

planets_r_w = [(3, 2*pi/3), (4, 2*pi/4), (5, 2*pi/5)]

def planetsPositions():
    def func(x):
        return [15.0*sin(4*pi*x/15.0)-20.0*sin(pi*x/10.0)-12.0*sin(pi*x/6.0)]
    root = fsolve(func, [10.0])
    return [polToCart(r, w, root[0]) for r, w in planets_r_w]

def plotPlanetsPositions(planets_xy):
    figure, axes = plt.subplots(1) 
    axes.set_xlim([-5, 5])
    axes.set_ylim([-5, 5])
    axes.set_aspect(1) 
    axes.scatter([0], [0], color='red')

    for r,_ in planets_r_w:
        axes.plot(*circle(r)) 

    planets_x, planets_y = list(zip(*planets_xy))
    axes.scatter(planets_x, planets_y, color=['blue', 'orange', 'green'])
    plt.show()

plotPlanetsPositions(planetsPositions())

The diagram below shows the positions of the planets when they are collinear next.