Flowfree | Vamshi Jandhyala

Game

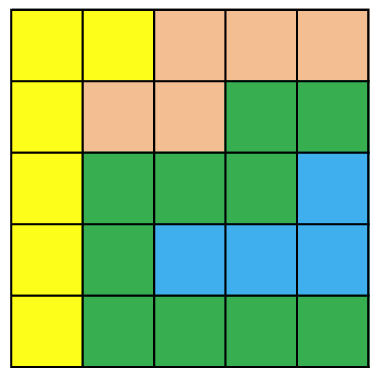
Flowfree is a puzzle game that is available as an android/ios app and online. The game is played on a square grid with $n$ pairs of same-colored squares. The objective is to join each of the same-colored pairs by means of an unbroken chain of squares of the same color. A typical starting position together with the solution is in shown in the figure below:

IP Formulation

Define the sets $M = 1...m$ and $N = 1...n$ , where $m$ is the size of the grid and $n$ is the number of pairs of same-colored cells. Also define variables $x_{ijk}=1$ if cell $(i,j)$ requires color $k$ , otherwise $0$ , $∀i ∈ M, j ∈ M, k ∈ N$ and parameters $S_{ijk}=1$ if cell $(i,j)$ has color $k$ , otherwise $0$ . The conditions required by the puzzle are enforced as follows.

Ensure the solution is consistent with the starting configuration.

x_{ijk} ≥ S_{ijk}, ∀ i ∈ M, j ∈ M, k ∈ N

Each cell contains a single color.

\sum_{k \in N} x_{ijk} = 1, ∀ i ∈ M, j ∈ M

Ensure a continuous chain for each color. This is done by ensuring that the initially colored squares have exactly one adjacent square of the same color and all other squares will have exactly two adjacent squares of the same color. Define

f(x_{ijk}) = \sum_{p=i−1 \\\\ p \neq i \\\\ p \in M}^{i+1} x_{pjk} + \sum_{q=j−1 \\\\ q\neq j \\\\ q \in M}^{j+1} x_{iqk} + S_{ijk} \\\\ f(x_{ijk}) ≥ 2x_{ijk}−5(1−x_{ijk}), ∀ i∈M, j∈M, k∈N \\\\ f(x_{ijk}) ≤ 2x_{ijk}+5(1−x_{ijk}), ∀ i∈M, j∈M, k∈N

Python code using OR-Tools

Here is the code for the above formulation and puzzle:

from ortools.sat.python import cp_model
from enum import IntEnum

class Color(IntEnum):
    YELLOW = 0,
    BROWN = 1,
    GREEN = 2,
    BLUE = 3

def puzzle():    
    m, n = 5, 4
    s = {(i,j,k):0 for i in range(m) for j in range(m) for k in range(n)}
    s[(0, 1, Color.YELLOW)], s[(4, 0, Color.YELLOW)] = 1, 1
    s[(0, 4, Color.BROWN)], s[(1, 1, Color.BROWN)] = 1, 1
    s[(3, 2, Color.BLUE)], s[(2, 4, Color.BLUE)] = 1, 1
    s[(1, 4, Color.GREEN)], s[(4, 4, Color.GREEN)] = 1, 1
    return m, n, s

def flowfree(puzzle):
    m, n, s = puzzle
    model = cp_model.CpModel()
    x = {(i,j,k): model.NewIntVar(0, 1, 'x(%i,%i,%i)' % (i,j,k)) 
            for i in range(m) for j in range(m) for k in range(n)}

    for i in range(m):
        for j in range(m):
            for k in range(n):
                model.Add(x[(i,j,k)] >= s[(i,j,k)])

    for i in range(m):
        for j in range(m):
            model.Add(sum(x[(i,j,k)] for k in range(n))==1)

    M = list(range(m))
    for i in range(m):
        for j in range(m):
            for k in range(n):
                f = s[(i,j,k)] + \
                    sum(x[(p,j,k)] for p in range(i-1, i+2) if p != i and p in M) + \
                    sum(x[(i,q,k)] for q in range(j-1, j+2) if q != j and q in M) 
                model.Add(f >= 2*x[(i,j,k)]-5*(1-x[(i,j,k)]))
                model.Add(f <= 2*x[(i,j,k)]+5*(1-x[(i,j,k)]))

    solver = cp_model.CpSolver()
    status = solver.Solve(model)
    if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
        for i in range(m):
            print(" ".join(str(Color(k)).ljust(15) for j in range(m) for k in range(n) 
                            if solver.Value(x[(i,j,k)]) != 0))
    else:
        print("Couldn't solve.")

flowfree(puzzle())

The output of the above program is as follows:

Color.YELLOW    Color.YELLOW    Color.BROWN     Color.BROWN     Color.BROWN    
Color.YELLOW    Color.BROWN     Color.BROWN     Color.GREEN     Color.GREEN    
Color.YELLOW    Color.GREEN     Color.GREEN     Color.GREEN     Color.BLUE     
Color.YELLOW    Color.GREEN     Color.BLUE      Color.BLUE      Color.BLUE     
Color.YELLOW    Color.GREEN     Color.GREEN     Color.GREEN     Color.GREEN

Who Betrayed Dune’s Duke Leto?

Riddle of the pilgrims