Puzzle
John Horton Conway defines a “quintomino” as a regular pentagon whose edges (or triangular segments) are colored with five different colors, one color to an edge. Not counting rotations and reflections as being different, there are 12 distinct quintominoes. Letting 1, 2, 3, 4, 5 represent the five colors, the 12 quintominoes can be symbolized as follows:
A. 12345 E. 12534 J. 13425
B. 12354 F. 12543 K. 13524
C. 12435 G. 13245 L. 14235
D. 12453 H. 13254 M. 14325
The numbers indicate the cyclic order of colors going either clockwise or counterclockwise around the pentagon. In 1958 Conway asked himself if it was possible to color the edges of a regular dodecahedron in such a way that each of the 12 quintominoes would appear on one of the solid’s 12 pentagonal faces. He found that it was indeed possible. In this post, we solve the puzzle using constraint programming.
Those who like to make mechanical puzzles can construct a cardboard model of a dodecahedron with small magnets glued to the inside of each face. The quintominoes can be cut from metal and colored on both sides (identical colors opposite each other) so that any piece can be “reflected” by turning it over. The magnets, of course, serve to hold the quintominoes on the faces of the solid while one works on the puzzle. The problem is to place the 12 pieces in such a way that the colors match across every edge. Without such a model, the Schlegel diagram of a dodecahedron can be used. This is simply the distorted skeleton of the solid, with its back face stretched to become the figure’s outside border. The edges are to be labeled (or colored) so that each pentagon (including the one delineated by the pentagonal perimeter) is a different quintomino.
Code walkthrough for Conway’s Dodecahedron-Quintomino Puzzle
Structural Setup
def create_dodecahedron_structure():
vertices = np.array([
[0.1988249522580409, -0.2736590696265117],
[-0.32170553056508533, 0.10452846326765347],
[0.32170553056508533, 0.10452846326765347],
[-0.1988249522580409, -0.2736590696265117],
[2.0712525571522672e-17, 0.3382612127177165],
# ... other vertices
])
pentagons_by_edges = [
[28,24,14,13,22],
[22,12,11,20,29],
# ... other pentagons
]
vertices_to_edge = {
(0,3):0,
(1,3):1,
# ... other vertex pairs
}
return vertices, vertices_to_edge, pentagons_by_vertices, pentagons_by_edges
Core Solving Function
Let’s break down the solve_dodecahedron_puzzle function in detail:
def solve_dodecahedron_puzzle(pentagons, quintominoes):
solver = Solver()
# Create 30 integer variables for edges (1-5)
edges = [Int(f"e{i}") for i in range(30)]
for e in edges:
solver.add(1 <= e, e <= 5)
- The function takes two parameters:
pentagons: List of lists containing edge indices for each pentagonquintominoes: List of valid quintomino patterns
- We create 30 integer variables (one for each edge) using Z3’s
Int()function - Each edge must be colored with a value from 1 to 5 (representing different colors)
Assignment Tracking
# Create variables to track which quintomino is used for each face
assignments = [Int(f"assign_{i}") for i in range(12)]
# Each assignment must be a valid quintomino index
for assign in assignments:
solver.add(0 <= assign, assign < 12)
# Each quintomino must be used exactly once
solver.add(Distinct(assignments))
This section:
- Creates 12 variables to track which quintomino is assigned to each face
- Ensures each assignment is valid (0-11, representing the 12 quintominoes)
- Uses Z3’s
Distinct()to ensure each quintomino is used exactly once
Pattern Matching Logic
# For each pentagon in the dodecahedron
for i, pentagon in enumerate(pentagons):
pentagon_edges = [edges[j] for j in pentagon]
# Create conditions for matching with assigned quintomino
match_conditions = []
for j, target in enumerate(quintominoes):
# Try all rotations of this target
rotation_conditions = []
for rot in range(5):
rotated = target[rot:] + target[:rot]
rotation_conditions.append(And([pentagon_edges[k] == rotated[k] for k in range(5)]))
# If this quintomino is assigned, one of its rotations must match
match_conditions.append(Implies(assignments[i] == j, Or(rotation_conditions)))
# One of these conditions must be true
solver.add(And(match_conditions))
This is the core pattern matching logic:
- For each pentagon face:
- Gets the edge variables for that face
- For each possible quintomino pattern:
- Tries all possible rotations of the pattern
- Creates conditions that match edge colors to pattern colors
- Uses
Implies()to connect pattern assignment with color matching
- Ensures that the assigned pattern actually matches the face
Solution Extraction
if solver.check() == sat:
model = solver.model()
edge_values = {i:model[e].as_long() for i,e in enumerate(edges)}
pentagon_mapping = {i: model[assignments[i]].as_long() for i in range(12)}
return edge_values, pentagon_mapping
return None, None
Finally, we:
- Check if a solution exists
- Extract the solution from Z3’s model
- Return:
- Edge color assignments
- Mapping of pentagons to quintomino patterns
Key Insights about the Solution
-
Constraint Satisfaction Approach
- Uses Z3’s powerful constraint solver
- Handles complex geometric and combinatorial constraints efficiently
- Explores the solution space systematically
-
Pattern Matching
- Considers all possible rotations of each quintomino
- Ensures edge colors match across shared edges
- Maintains uniqueness of pattern assignments
-
Solution Verification
- Each edge gets exactly one color
- Each face shows a different quintomino pattern
- All patterns are used exactly once
- Colors match across shared edges
-
Visualization
- Shows both the individual patterns and complete solution
- Uses color coding for clear pattern recognition
- Provides face labels for pattern identification
Puzzle solution
Here are the twelve quintominoes and the solution to the puzzle.
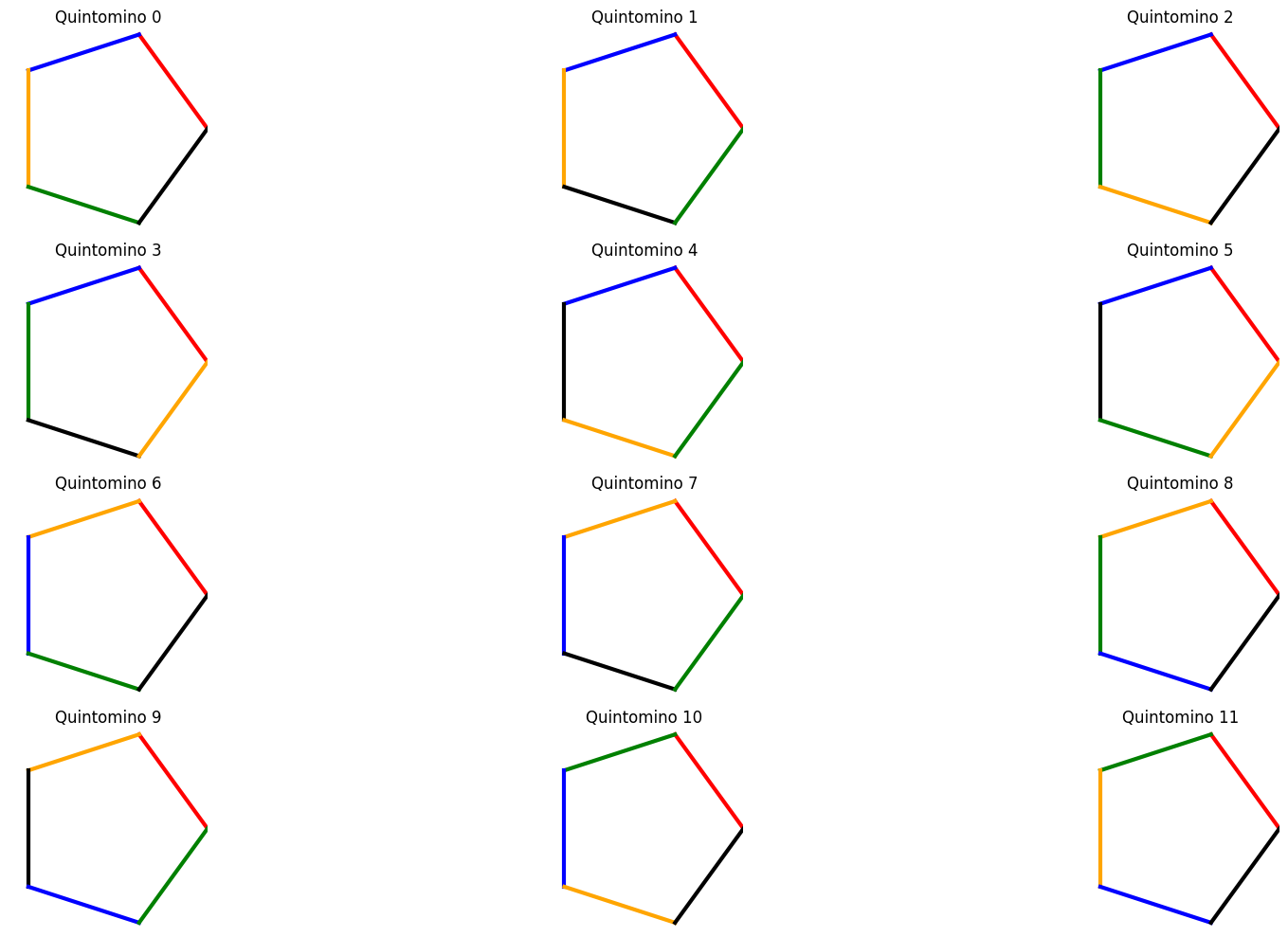
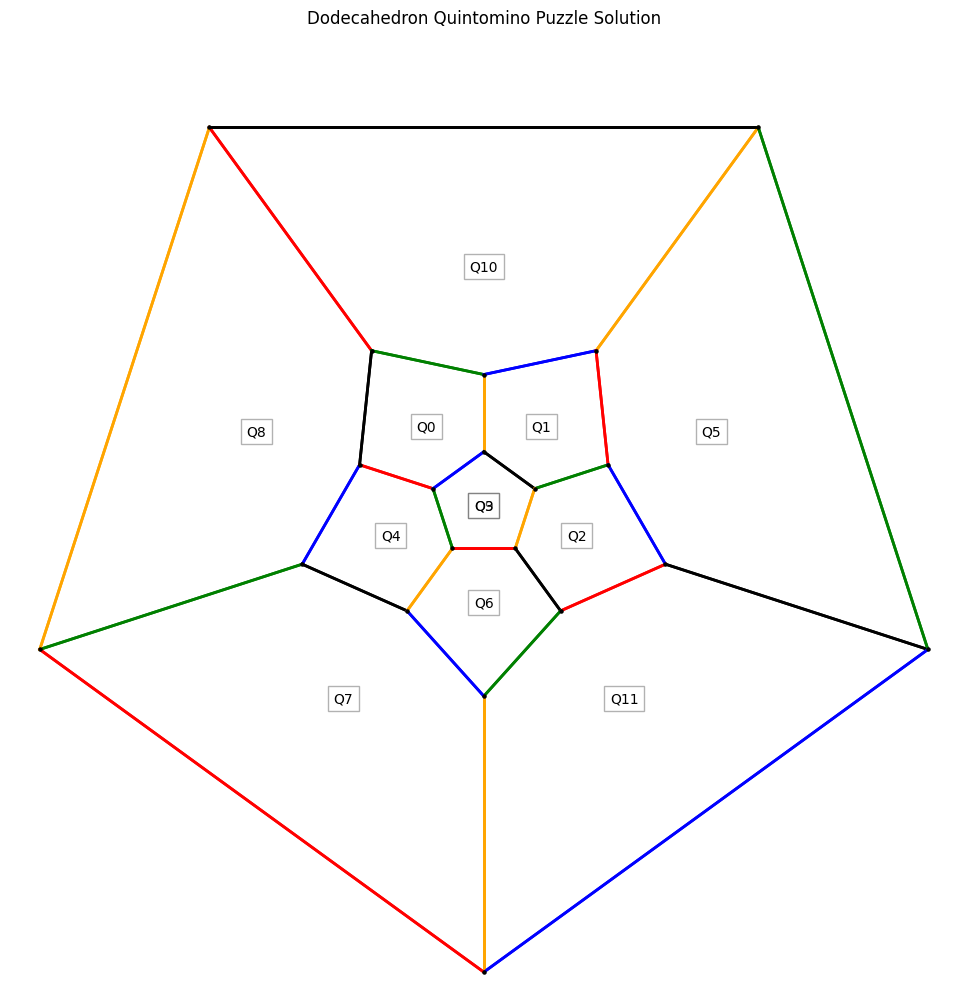
Complete code listing
import matplotlib.pyplot as plt
import numpy as np
from z3 import *
def create_dodecahedron_structure():
vertices = np.array([
[0.1988249522580409, -0.2736590696265117],
[-0.32170553056508533, 0.10452846326765347],
[0.32170553056508533, 0.10452846326765347],
[-0.1988249522580409, -0.2736590696265117],
[2.0712525571522672e-17, 0.3382612127177165],
[0.4861518423097248, -0.6691306063588582],
[-0.7866102045505139, 0.25558514871625726],
[0.7866102045505139, 0.25558514871625726],
[-0.4861518423097248, -0.6691306063588582],
[5.064471210039385e-17, 0.8270909152852017],
[1.1498814685531944, -0.3736191374661521],
[-1.1498814685531944, -0.3736191374661521],
[0.7106658305995175, 0.9781476007338056],
[-7.403338475342e-17, -1.2090569265353068],
[-0.7106658305995174, 0.9781476007338056],
[2.8116038154478655, -0.9135454576426009],
[-2.8116038154478655, -0.9135454576426009],
[1.7376667208456678, 2.391693058376407],
[-1.810208727905995e-16, -2.9562952014676114],
[-1.7376667208456673, 2.391693058376407]
])
pentagons_by_edges =[
[28,24,14,13,22],
[22,12,11,20,29],
[20,10,19,23,25],
[23,18,17,21,26],
[21,16,15,24,27],
[16,17,8,1,6],
[6,2,9,14,15],
[3,7,12,13,9],
[10,11,7,4,5],
[5,0,8,18,19],
[0,4,3,2,1],
[28,27,26,25,29]]
pentagons_by_vertices =[
[19,17,12,9,14],
[12,17,15,10,7],
[10,15,18,13,5],
[13,18,16,11,8],
[11,16,19,14,6],
[11,6,1,3,8],
[1,6,14,9,4],
[2,4,9,12,7],
[10,5,0,2,7],
[0,5,13,8,3],
[0,3,1,4,2],
[19,17,15,18,16]]
vertices_to_edge = {
(0,3):0,
(1,3):1,
(1,4):2,
(2,4):3,
(0,2):4,
(0,5):5,
(1,6):6,
(2,7):7,
(3,8):8,
(4,9):9,
(5,10):10,
(7,10):11,
(7,12):12,
(9,12):13,
(9,14):14,
(6,14):15,
(6,11):16,
(8,11):17,
(8,13):18,
(5,13):19,
(10,15):20,
(11,16):21,
(12,17):22,
(13,18):23,
(14,19):24,
(15,18):25,
(16,18):26,
(16,19):27,
(17,19):28,
(15,17):29
}
return vertices, vertices_to_edge, pentagons_by_vertices, pentagons_by_edges
def solve_dodecahedron_puzzle(pentagons, quintominoes):
solver = Solver()
# Create 30 integer variables for edges (1-5)
edges = [Int(f"e{i}") for i in range(30)]
for e in edges:
solver.add(1 <= e, e <= 5)
# Create variables to track which quintomino is used for each dodecahedron pentagon
assignments = [Int(f"assign_{i}") for i in range(12)]
# Each assignment must be a valid quintomino index
for assign in assignments:
solver.add(0 <= assign, assign < 12)
# Each quintomino must be used exactly once
solver.add(Distinct(assignments))
# For each pentagon in the dodecahedron
for i, pentagon in enumerate(pentagons):
pentagon_edges = [edges[j] for j in pentagon]
# Create conditions for matching with assigned quintomino
match_conditions = []
for j, target in enumerate(quintominoes):
# Try all rotations of this target
rotation_conditions = []
for rot in range(5):
rotated = target[rot:] + target[:rot]
rotation_conditions.append(And([pentagon_edges[k] == rotated[k] for k in range(5)]))
# If this quintomino is assigned, one of its rotations must match
match_conditions.append(Implies(assignments[i] == j, Or(rotation_conditions)))
# One of these conditions must be true
solver.add(And(match_conditions))
if solver.check() == sat:
model = solver.model()
edge_values = {i:model[e].as_long() for i,e in enumerate(edges)}
pentagon_mapping = {i: model[assignments[i]].as_long() for i in range(12)}
return edge_values, pentagon_mapping
return None, None
colors = {1:'red', 2:'blue', 3:'orange', 4:'green', 5:'black'}
def visualize_quintominoes(quintominoes):
fig = plt.figure(figsize=(20, 10))
for i, pentagon in enumerate(quintominoes):
ax = plt.subplot(4, 3, i+1)
angles = np.linspace(0, 2*np.pi, 6)[:-1]
points = np.array([[0.4*np.cos(angle) + 0.5, 0.4*np.sin(angle) + 0.5] for angle in angles])
for j in range(5):
start = points[j]
end = points[(j+1) % 5]
ax.plot([start[0], end[0]], [start[1], end[1]], color=colors[pentagon[j]], linewidth=3)
title = f'Quintomino {i}'
ax.set_title(title)
ax.set_xlim(0.1, 0.9)
ax.set_ylim(0.1, 0.9)
ax.axis('off')
ax.set_aspect('equal')
plt.tight_layout()
plt.show()
def visualize_solution(vertices, vertices_to_edge, pentagons_by_vertices, pentagon_mapping, edge_values):
print(edge_values)
fig = plt.figure(figsize=(20, 10))
ax = fig.add_subplot(1,1,1)
for pentagon_idx, pentagon in enumerate(pentagons_by_vertices):
for i in range(5):
v1, v2 = sorted([pentagon[i], pentagon[(i+1) % 5]])
color = colors[edge_values[vertices_to_edge[(v1,v2)]]]
ax.plot([vertices[v1][0], vertices[v2][0]], [vertices[v1][1], vertices[v2][1]], color=color, linewidth=2)
ax.scatter(vertices[:,0], vertices[:,1], color='black', s=5, zorder=5)
# Add pentagon labels
for idx, pentagon in enumerate(pentagons_by_vertices):
center = np.mean([vertices[v] for v in pentagon], axis=0)
ax.text(center[0], center[1], f'Q{pentagon_mapping[idx]}',
ha='center', va='center',
bbox=dict(facecolor='white', edgecolor='black', alpha=0.3))
ax.set_title('Dodecahedron Quintomino Puzzle Solution')
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.axis('off')
ax.set_aspect('equal')
plt.tight_layout()
plt.show()
def solve_and_show():
quintominoes = [
[1, 2, 3, 4, 5],
[1, 2, 3, 5, 4],
[1, 2, 4, 3, 5],
[1, 2, 4, 5, 3],
[1, 2, 5, 3, 4],
[1, 2, 5, 4, 3],
[1, 3, 2, 4, 5],
[1, 3, 2, 5, 4],
[1, 3, 4, 2, 5],
[1, 3, 5, 2, 4],
[1, 4, 2, 3, 5],
[1, 4, 3, 2, 5]
]
vertices, vertices_to_edge, pentagons_by_vertices, pentagons_by_edges = create_dodecahedron_structure()
edge_values, pentagon_mapping = solve_dodecahedron_puzzle(pentagons_by_edges, quintominoes)
if edge_values:
visualize_quintominoes(quintominoes)
visualize_solution(vertices, vertices_to_edge, pentagons_by_vertices, pentagon_mapping, edge_values)
else:
print("No solution exists")
solve_and_show()