Inversion - A beautiful idea from Geometry

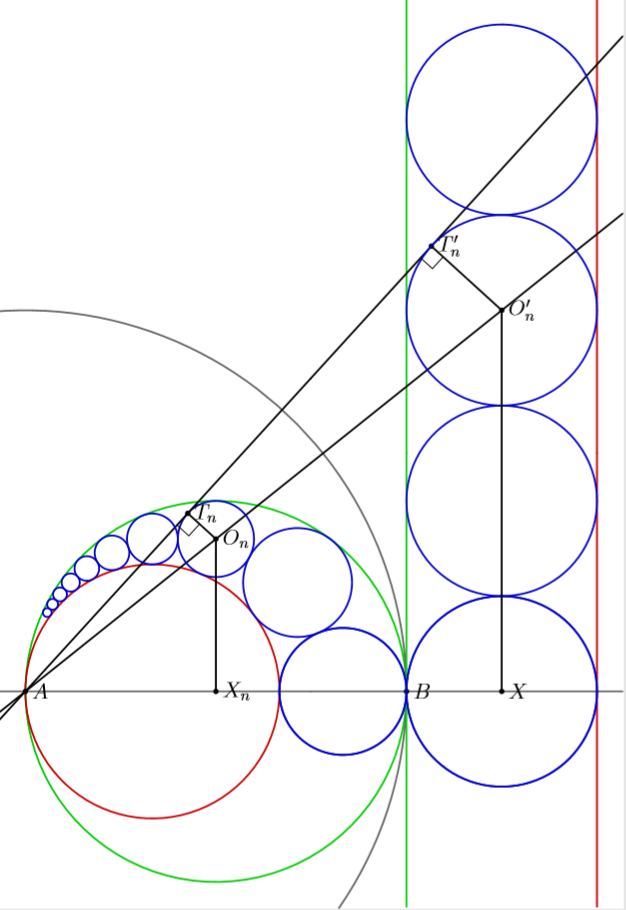
Problem

There are $3$ semi circles and infinite circles in this figure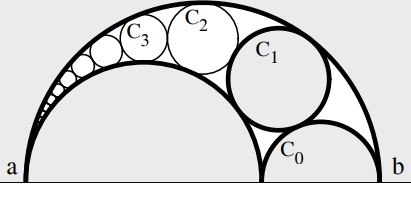

$R_0$ is the radius of semicircle $C_0$ is $\frac{1}{6}ab$. Prove that $Y_n$ (height of the center of the $n^{th}$ circle) is $2nR_n$.

Solution

Using the circle whose centre is $A$ and radius is $AB$ as the circle of inversion in the figure

we can see that the red and green circles get inverted to the red and green parallel lines.

This follows from the following properties of inversion:

1. Circles that pass through $O$ (the centre of inversion) are inverted to “lines”. If that circle also passes through $k$ (the circle of inversion) at two points $P$ and $Q$, its inversion will be the “line” passing through $P$ and $Q$. If a circle passes through $O$ and is internally tangent to $k$, its inverse will be the “line” externally tangent to $k$.

2. A “line” that passes through $O$ is inverted to itself. Note, of course that the individual points of the “line” are inverted to other points on the “line” except for the two points where it passes through $k$.

3. Two “Circles” that intersect in zero, one, or two places are inverted to other “circles” that intersect in the same number of places. A little care must be taken to interpret this statement correctly if the intersection or tangency is at $O$. For example, if two circles are tangent at $O$, then their inverses will be two parallel “lines” (that “meet at infinity”). If a line and a circle are tangent at $O$, then the inverse of the circle will be parallel to the line (which is inverted into itself).

4. A “circle” intersecting or tangent to $k$ is inverted to a “circle” intersecting or tangent to $k$ in exactly the same places or place.

Let $O_n$ be the centre of the $n^{th}$ circle $C_n$ and $O_n'$ be the inverted point of $O_n$.

From the similar triangles $AO_nT_n$ and $AO_n'T_n'$ we have

Let $X_n$ be the projection of $C_n$ on the line $AB$ and $X$ be the projection of $C_n'$ on $AB$.

From the similar triangles $AO_nX_n$ and $AO_n'X$ we have

From the above two equations we have,

where $R_0'$ is the radius of the inverted circle of $C_0$.

Problem

Consider three circles that are mutually and externally tangent to each other. We now draw two circles, one circumscribing and one inscribed between the three circles. If the three circles have radii $1,2$ and $3$ respectively, what is the distance between the centres of the circumscribing and inscribed circles?

Solution

Let the centers of the circles of radii $1,2$ and $3$ be at $A(-1,0),D(-1,3)$ and $C(3,0)$ respectively as shown in the figure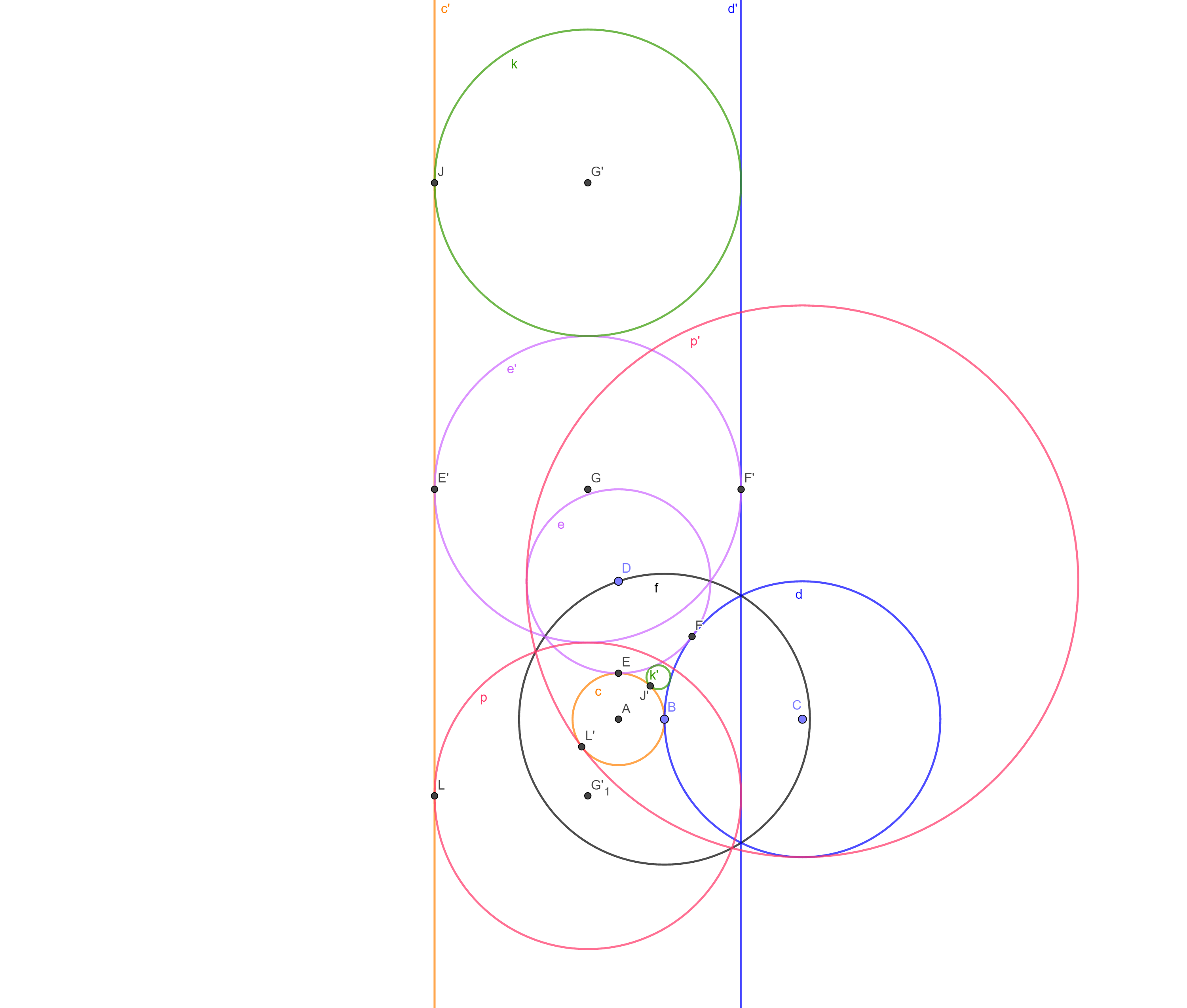

We choose the circle of inversion $f$ such that it passes through $D$ and is centered at $B(0,0)$ (which is the point of tangency of circles $c$ and $d$ centered at $A$ and $C$).Therefore, the radius of the inverting circle $f$ is $\sqrt{10}$.

The circles $c$ and $d$ get inverted to parallel lines $c'$ and $d'$. The circle $e$ is inverted to $e'$. The inverted circles $k$ and $p$ of the circles $k'$ and $p'$ which are internally and externally tangent to circles $c$, $d$ and $e$ will be tangent to the lines $c'$ and $d'$ and the circle $e'$.

If the center of the circle of inversion is at $(h,k)$ and it’s radius is $r$, then a point $(x,y)$ is inverted to a point $(\frac{(x-h)r^2}{(x-h)^2+(y-k)^2} + h,\frac{(y-k)r^2}{(x-h)^2+(y-k)^2} + k)$.

$E(-1,1)$, the point of tangency of circles $c$ and $e$ gets inverted to $E'(-5,5)$. $F$ divides line segment $CD$ in the ratio $2:3$, therefore coordinates of $F$ are $(\frac{3}{5},\frac{9}{5})$.$F$ gets inverted to $F'(\frac{5}{3},5)$. The radius of the circle $e'$ is half of the length of the line segment $E'F'$ = $\frac{10}{3}$.

$J(-5,\frac{35}{3})$, the point of tangency of $k$ and $c'$ will be inverted to $J'(\frac{-9}{29},\frac{21}{29})$ the point of tangency of $k'$ and $c$. The coordinates of $G'$ are $(-\frac{5}{3},\frac{35}{3})$. The center of circle $k'$ lies on the lines $BG'$ and $AJ'$. The equation of the line $AJ'$ is $\frac{y-0}{\frac{21}{29}} = \frac{x+1}{\frac{20}{29}}$. The equation of the line $BG'$ is $\frac{y}{\frac{35}{3}} = \frac{x}{-\frac{5}{3}}$. Solving the above two equations, we see that the center of the circle $k'$ is $(-\frac{3}{23},\frac{21}{23})$.

$L(-5,-\frac{5}{3})$, the point of tangency of $p$ and $c'$ will be inverted to $L'(-\frac{9}{5}, -\frac{3}{5})$ the point of tangency of $p'$ and $c$.The cooridnates of $G_1'$ are $(-\frac{5}{3},-\frac{5}{3})$.The center of circle $p'$ lies on the lines $BG_1'$ and $AL'$. The equation of the line $AL'$ is $\frac{y-0}{-\frac{3}{5}} = \frac{x+1}{-\frac{4}{5}}$.The equation of the line $BG_1'$ is $\frac{y}{-\frac{5}{3}} = \frac{x}{-\frac{5}{3}}$. Solving the above two equations, we see that the center of the circle $p'$ is $(3,3)$.

Therefore the distance between the centers is $\sqrt{(3+\frac{3}{23})^2 + (3-\frac{21}{23})^2} = \frac{24 \sqrt{13}}{23}$ .